El mejor camino para conseguir un buen diseño es generar varios diseños y seleccionar el mejor. Para conseguir el mejor diseño se deben analizar y evaluar los diseños.
Cómo se analiza y se evalúa un diseño? Una opción es construir el sistema y examinarlo. Esto es apropiado cuando el diseño es para un sistema pequeño, pero es impracticable para sistemas grandes. La mayoría de procesos químicos son sistemas a gran escala y es impracticable construir físicamente el sistema para su análisis. Por lo tanto los ingenieros químicos deben buscar otras formas para examinar los sistemas (procesos).
En cada caso particular, un modelo matemático es construido de acuerdo a los objetivos del proceso y estudio del mismo, la exactitud deseada, y la confianza en los datos usados. Esto es usualmente un proceso secuencial, así una formulación inicial es desarrollada, pasando por una continua y progresiva reformulación.
2.1 LOS MODELOS EN INGENIERIA QUIMICA (MODELOS BASADOS EN LOS PRINCIPIOS DE FENOMENOS DE TRANSPORTE)
El intento de los hombres para encontrar una explicación unificada de los fenómenos naturales, sin duda, es muy antigua. Los jónicos trataron de explicar totalmente tales fenómenos en función de la modificación del comportamiento de una sustancia básica, tal como agua o aire. Consideremos lo que habitualmente denominamos propiedades de la materia, por ejemplo; los conceptos de calor específico, conductividad calorífica, viscosidad, coeficiente de difusión, resistencia, presión y temperatura. Una de las principales diferencias entre la actitud de un físico y un ingeniero frente a estas propiedades reside en la forma en las que tratan estos conceptos.
Un físico no está satisfecho debido a que estos conceptos no son suficientemente elementales. Su actividad está dirigida hacia el intento de explicar estos conceptos por un número reducido de otros conceptos más elementales, tales como núcleos, átomos y electrones. Tampoco el ingeniero se encuentra satisfecho, pero por razones totalmente diferentes. Para la mayor parte de los problemas ingenieriles estos conceptos de propiedades son demasiado elementales. En vez de tratar de encontrar sub-elementos más pequeños; como le ocurre al físico, el ingeniero desearía integrarlos en conceptos más elaborados. Aunque estos conceptos pueden parecer sencillos; en la práctica no ocurrirá así puesto que el ingeniero los utilizará en una u otra forma según resulten más convenientes. El problema básico del ingeniero consistirá en considerar aspectos particulares que describan de una forma precisa y convincente el comportamiento de los procesos macroscópicos.
Tabla 2.1 Estrato de tallado de principios fisicoquímicos
| Estrato de descripción fisicoquímica | Utilización por los ingenieros | Descripciones matemáticas | Parámetros típicos para análisis |
| Atómico y molecular | Formación fundamental | Trata cantidades discretas: mecánica cuántica, mecánica estadística, teoría cinética | Funciones de distribución; integrales de colisión |
| Microscópico | Aplicable solamente a casos especiales | Fenómenos de trans-porte laminar, teorías estadísticas de la turbulencia | Coeficientes fenomenológicos; coeficientes de viscosidad, difusión, conducción calorífica; coeficiente de soret |
| Gradiente múltiple | Aplicable solamente a casos especiales | Fenómenos de transporte laminar y turbulento; transporte en medios porosos | Coeficientes de transporte “efectivo |
| Gradiente máximo | Utilizado para sistemas de flujo continuo; “flujo de pistón” | Fenómenos de transporte laminar y turbulento, diseño de reactores | Coeficientes de transporte de interfase, constantes cinéticas |
| Macroscópico | Utilización muy amplia | Ingeniería de procesos, operaciones básicas; termodinámica y cinética clásicas | Coeficientes de transporte de interfase; constantes cinéticas macroscópicas; factores de fricción |
Esto no quiere decir que el ingeniero deba apartarse de las ciencias fundamentales, puesto que constituyen el fundamento de su trabajo, y, en muchos casos, deberá utilizar conocimientos directamente obtenidos por físicos y químicos. Por ejemplo, a temperaturas elevadas la capacidad calorífica de gases se puede predecir a partir de consideraciones de mecánica estadística, en situaciones en las que sería más difícil obtener datos empíricos. Pero los ingenieros tratan más frecuentemente con conceptos y propiedades de tipo compuesto, así como también con variables, que son las variables de manipulación, aunque pueden no ser las variables verdaderas de un proceso. El ingeniero realiza el mismo tipo de análisis que el físico: toma un conjunto de datos, los analiza y elabora reglas, pero se mueve en una escala diferente dentro del mundo real.
Uno de los objetivos de este capítulo es presentar brevemente los modelos que se obtienen a partir de los principios fisicoquímicos (principios de los fenómenos de transporte) los cuales constituyen el núcleo fundamental de los modelos utilizados por los ingenieros. Aquí se clasifican los modelos de acuerdo con la estructura de la Tabla 2.1, en la cual la primera columna muestra los distintos niveles de descripción utilizados para representar matemáticamente los procesos reales. Las demás columnas de la tabla sirven para identificar e interpretar estas categorías en una terminología más familiar. Estos niveles de estratos están relacionados con la complejidad del detalle físico interno que se incluye en la descripción del proceso: el grado de detalle disminuye a medida que se desciende en la tabla. Téngase en cuenta que solamente disminuye el detalle interno del sistema al descender en las columnas de la tabla y no, en cambio, la fidelidad de representación del proceso real por el modelo. Por ejemplo un modelo macroscópico puede representar mejor un determinado proceso que un modelo más detallado. Los principios básicos correspondientes a los modelos no son más que los conceptos de balance de materia, cantidad de movimiento y energía. Como se vera en los próximos capítulos, cada balance puede representarse en esta forma:
El objetivo general del modelo es reemplazar estas palabras por expresiones matemáticas que sean tan rigurosas y a la vez contengan pocos parámetros desconocidos como sea posible.
Para formar un modelo completo es necesario disponer de dos condicionamientos matemáticos:
a) Las ecuaciones algebraicas o diferenciales que lo rigen
b) Las adecuadas condiciones iniciales y límite
2.1.1 Descripción molecular
La descripción más fundamental de los procesos debiera basarse sobre consideraciones moleculares. La descripción molecular se caracteriza porque trata un sistema arbitrario como si estuviese compuesto de entidades individuales, cada una de las cuales siguen ciertas leyes. En consecuencia, las propiedades y las variables de estado del sistema se obtienen como suma de todas las entidades. La mecánica cuántica, la mecánica estadística de equilibrio y no-equilibrio, así como la mecánica clásica, constituirán métodos típicos de análisis, mediante los cuales se podrían calcular teóricamente todas las propiedades y formas de respuesta del sistema. Sin embargo, estos campos implican tales complejidades matemáticas que, para los fines ingenieriles, no son posible por ahora desarrollarlos hasta un estado que permita al ingeniero utilizar estos conceptos en el análisis y diseño, excepto para ciertos casos muy especiales, como por ejemplo el efecto sobre gases diluidos de temperaturas muy bajas o muy elevadas. Por consiguiente, para nuestros fines, la descripción molecular no encuentra mucha aplicación directa. Debido a este hecho, y a la gran complejidad ya mencionada, no se insistirá aquí en la descripción molecular.
2.1.2 Descripción microscópica
Una clase de modelos con fundamento básico algo menor, corresponde a los que llamaremos descripción microscópica. Corresponde a un tratamiento fenomenológico del problema y admite que el sistema puede considerarse como continuo. En otras palabras, se ignoran las interacciones moleculares detalladas y se plantean ciertas ecuaciones de balance diferencial para materia, cantidad de movimiento y energía. Para procesos no fluyentes o para procesos con flujo laminar, este estado de descripción encuentra numerosas aplicaciones prácticas, aunque con frecuencia, resulta excesivamente complicado. Para flujo turbulento y elevado grado de mezcla (que son casos de interés primario) se puede utilizar la teoría estadística de la turbulencia. Pero, lo mismo que ocurre con los conceptos de la mecánica estadística, tal tratamiento de un proceso no encuentra mucha aplicación práctica y es necesario recurrir a otros métodos de descripción. Un tratamiento muy completo se puede encontrar en el libro de Bird, Steward y Lightfoot. Así mismo se pueden encontrar una serie de modelos generalizados en el libro de Himmelblau y Bischoff.
2.1.3 Descripción de gradiente múltiple
Tal como se indica en la Tabla 2.1, el siguiente nivel para la descripción de un proceso por modelos del tipo de fenómenos de transporte lo denominaremos nivel de gradiente múltiple. Este nivel incorpora menos información detallada acerca de las características internas del sistema que en el caso de la descripción microscópica. Las formas de las ecuaciones matemáticas están sugeridas y corresponden a las ecuaciones de transporte microscópico, pero con coeficientes modificados. Estos coeficientes son evidentemente empíricos y deben determinarse para cada tipo de equipo o unidad de interés, si bien es preciso indicar que, utilizando las correlaciones adecuadas, los coeficientes obtenidos en unas determinadas circunstancias pueden con frecuencia resultar útiles en otras distintas si el ingeniero procede con las debidas precauciones. La característica esencial de la descripción de gradiente múltiple es que son importantes uno o más términos de descripción que deben ser retenidos en el modelo, con o sin los términos convectivos. El modelo de gradiente múltiple encuentra aplicaciones en procesos con flujo turbulento o en flujos con pasos muy complicados como el que tienen lugar en lechos de relleno o medios porosos, procesos en los que no se puede medir ni calcular el campo de velocidad local. En el libro de Himmelblau y Bischoff, se pueden encontrar modelos de gradiente múltiple desarrollados a partir de los balances microscópicos.
2.1.4 Descripción de gradiente máximo
Pasamos ahora a una forma todavía menos detallada de descripción, que es la descripción de gradiente máximo. En cierto sentido, este modelo se puede considerar como un modelo simplificado de gradiente múltiple en el que se suprimen los términos de dispersión y solamente se conserva una derivada en los términos de flujo global. Sin embargo, el modelo se emplea con tal frecuencia que ha adquirido una categoría independiente. Con frecuencia el ingeniero no intenta analizar el detalle interno de los modelos de gradiente múltiple. Se realizan entonces suposiciones simplificables adicionales con lo cual se obtienen ecuaciones matemáticas de fácil tratamiento que resultan, no obstante, muy satisfactorias para numerosos fines. En el modelo de máximo gradiente se desprecia toda la dispersión y solamente el mayor componente (unidimensional) del gradiente de la variable independiente se considera en cada balance. Por ejemplo en la representación de gradiente máximo de un reactor químico o en sistemas de absorción de gases, solamente se consideran los gradientes de concentración en la dirección axial originados por el flujo global, mientras que los gradientes radiales, la dispersión, etc. Se ignoran.
 |
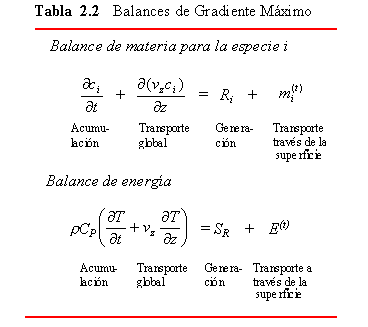Los modelos de gradiente máximo son generalmente los modelos considerados en los libros elementales para los procesos continuos y se relacionan en la Tabla 2.2. El modelo de máxima gradiente se denomina con frecuencia modelo de “flujo en pistón” en la mayoría de textos.
La descripción de gradiente máximo reduce los principios fisicoquímicos a ecuaciones diferenciales menos detalladas que se pueden desarrollar simplificando las ecuaciones de balances microscópicos. El balance de cantidad de movimiento se ignora puesto que normalmente se supone que la velocidad es constante o bien una función sencilla de z. En el balance de energía, el término SR representa la energía neta desprendida por el proceso durante la reacción(es) que se representa por Ri en el balance(s) de materia. El término 
tiene en cuenta la velocidad de transferencia molar, por unidad de volumen de la especie i, a través de los límites del sistema de área S ( 
es positivo cuando se introduce materia). En el balance de energía E(t) representa la transferencia de interfase de energía a través de los límites del sistema por uno o bien una combina0ción de los siguientes mecanismos: conducción, convección, radiación, trabajo mecánico o transferencia de materia que los acompaña. Finalmente, en el modelo de gradiente máximo es importante recordar que las concentraciones y temperaturas ya no son valores puntuales sino valores promediados para la sección transversal, y son funciones de una sola dirección coordenada.
2.1.5 Descripción macroscópica
Con frecuencia no se desea analizar un proceso con todo el detalle interno de los modelos de gradiente múltiple o máximo, sino que, en vez de esto, se expresa la descripción macroscópica ignorando todo detalle dentro del subsistema especificado y, en consecuencia, en el planteamiento matemático no intervienen gradientes espaciales. De hecho, de los balances generales, solamente el tiempo permanece como una variable diferencial independiente. Las variables dependientes, tales como concentración y temperatura, no son funciones de la posición y, por tanto, representan valores medios para todo el volumen del subsistema. Esta pérdida de detalle simplifica grandemente la descripción matemática. En este texto nos abocaremos principalmente al estudio de este tipo de modelos por su importancia en el análisis y diseño de los sistemas de control.
2.2 CONSTRUCCIÓN DEL MODELO.
Es la parte más delicada y crítica del modelamiento matemático. La construcción de cualquier modelo se inicia buscando información sobre el sistema en cuestión, luego se hace el análisis de cada “proceso elemental” que toma lugar en el sistema. Este análisis se realiza a condiciones bajo las cuales debe operar el sistema.
Para comenzar, es investigado el modelo de flujo de un proceso elemental para suministrar una base al modelo matemático. Después sigue la cinética de las reacciones químicas, transferencia de masa y energía las cuales son evaluadas a la luz del modelo de flujo ya antes fijado. Luego se efectúa una formulación matemática para cada proceso, y estas formulaciones individuales (usualmente en la forma de una función de transferencia) son combinadas para construir una descripción matemática total del sistema.tema.
Los siguientes grupos de ecuaciones pueden ser establecidos como base del modelo matemático basados en el comportamiento físico del sistema.
1. Balances de Masa y Energía, desarrollados sobre la base de modelos de flujo existentes. Estas ecuaciones describen las distribuciones de temperatura, composición y propiedades asociadas (tales como densidad, viscosidad, calor específico, etc.) en los flujos.
2. Ecuaciones para los procesos elementales, para elementos locales del fluido. Estas ecuaciones abarcan transferencia de masa y energía, reacciones químicas, etc.
3. Relaciones teóricas empíricas y semiempiricas, entre las diferentes variables del proceso, tales como la dependencia del coeficiente de transferencia de masa, de la velocidad de flujo. La dependencia del calor específico de una solución en la composición, etc.
4. Limitaciones sobre variables de proceso, en la construcción de un modelo para un proceso, se tiene que contar con limitaciones objetivamente impuestas sobre el rango de variación de algunas variables.
Al seleccionar un modelo, deben tenerse en cuenta los siguientes puntos:
- Un modelo debe representar completamente los flujos de materia y energía en términos de un simbolismo matemático lo suficientemente simple.
- Con sistemas heterogéneos, debe ser seleccionado un modelo para cada fase; los modelos pueden se iguales o diferentes.
- Con sistemas homogéneos, será suficiente un modelo de parámetros agrupados para cualquier propósito; con sistemas homogéneos, si es una fase continua puede adaptarse un modelo de parámetros agrupados y un modelo de parámetros distribuidos si es una fase dispersa.
- Cada fase de sistemas heterogéneos puede ser tratada separadamente.
Las ecuaciones usadas para la descripción matemática del proceso pueden ser:
Ecuaciones Finitas, son usualmente empleadas en la especificación matemática de las condiciones de estado estacionario (estáticas) en procesos tratados como sistemas de parámetros globalizados o agrupados (un ejemplo es un reactor CSTR).
Ecuaciones diferenciales ordinarias, son usadas en la descripción matemática de las condiciones no estacionarias (dinámica) en sistemas de parámetros agrupados, y también condiciones de estado estacionario en sistemas de parámetros distribuidos en el cual los parámetros dependen solamente de una coordenada en el espacio. En el primer caso, la variable independiente es el tiempo, y en la segunda, es la posición (coordenada).
Ecuaciones diferenciales parciales, son usadas en la descripción matemática para el comportamiento dinámico de sistemas de parámetros distribuidos o del comportamiento de un estado estacionario en el cual los parámetros son distribuidos en mas de una coordenada. En el caso general, la solución de ecuaciones diferenciales parciales en el estado no estacionario requiere el conocimiento de condiciones especificadas como funciones del tiempo en adición a las condiciones iniciales. En el caso del estado estacionario, solamente se necesita especificar las condiciones iniciales.
Ecuaciones de diferencia finita, usadas para modelar sistemas de parámetros agrupados al estado estacionario que ocurren por etapas, en este caso la solución toma valores discretos.
2.3 USO DE LOS MODELOS MATEMÁTICOS EN INGENIERÍA QUÍMICA
El resultado más importante al desarrollar un modelo de un sistema de ingeniería química, es el entendimiento que se consigue de lo que realmente es el proceso. Los modelos matemáticos se pueden usar en todas las fases de la ingeniería química, desde la investigación y desarrollo hasta la operación de la planta, y aun en los estudios económicos y de negocios.
1. Investigación y desarrollo: determinando los mecanismos y parámetros de la cinética química desde los datos de laboratorio o planta piloto para la reacción; explorando los efectos de las diferentes condiciones de operación para estudios de optimización y control; así como en cálculos de escalamiento.
2. Diseño: explorando los tamaños y arreglos de los equipos de proceso para una operación dinámica; estudiando la interacción de varias partes del proceso, particularmente cuando se usa reciclo de materiales o transferencia de calor; evaluando procesos alternativos, estrategias y estructuras de control; simulando la puesta en marcha, paradas abruptas y, situaciones y procedimientos de emergencia.
3. Operación de la Planta: problemas de control, entrenamiento de los operarios, optimizar la operación de la planta.
2.4 LEYES FUNDAMENTALES
En esta sección, se revisan algunas leyes de física y química en su forma general de dependencia del tiempo, y se ilustra su aplicación a algunos sistemas químicos simples.
2.4.1 Ecuaciones de Continuidad
A. ECAUCIÓN DE CONTINUIDAD TOTAL (BALANCE DE MASA). El principio de conservación de la masa cuando se aplica a un sistema dinámico es:
 |
Flujo de masa entrando al sistema |  |
— |  |
Flujo de masa saliendo del sistema |  |
= |  |
Velocidad de cambio de masa dentro del sistema |  |
(2.1) |
Las unidades de esta ecuación son masa por tiempo. Solamente una ecuación de continuidad total puede escribirse para un sistema. El lado derecho de la Ec. (2.1) será ya sea una derivada parcial 
o una derivada ordinaria 
de la masa dentro del sistema con respecto ala variable independiente t.
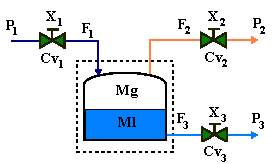
Ejemplo 2.1 Considerar el tanque de liquido perfectamente mezclado mostrado en la Fig. 2-1 hacia el cual entra liquido a un caudal de F0 (pies3/min. o m3/min.) y con una densidad de ro (lbm/ pies3 o Kg./ m3). La retención volumétrica de liquido en el tanque es V (pies3 o m3), y su densidad es r. El flujo volumétrico desde el tanque es F, y la densidad de la corriente de salida es la misma que la del contenido del tanque.
 |
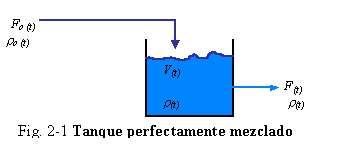El sistema para el cual queremos escribir una ecuación total de continuidad es toda la fase liquida en el tanque. Podemos definir como un sistema macroscópico, en oposición a un sistema microscópico está bien definido y es de tamaño finito. El balance de masa es para el tanque en su totalidad y, no solamente para un elemento diferencial del tanque. Aplicando las Ec. (1.12) y (2.1)
F0 ro – F r = velocidad de cambio de r V =d(r V)/dt (2.2)
Las unidades de esta ecuación son lbm/min. o Kg./min.
 |
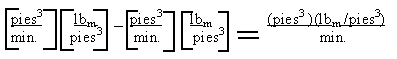Desde que el liquido es perfectamente mezclado, la densidad es la misma en cada punto dentro del tanque; esta no varía con la posición radial ni axial, por lo tanto no hay gradientes espaciales en el tanque. Esto es el porque podemos usar un sistema macroscópico. Esto también indica que existe una sola variable independiente, t.
Como r y V son funciones de t solamente, una derivada ordinaria es usada en la Ec. (2.2).
 |
Ejemplo 2.2 Fluido esta pasando a través de una tubería cilíndrica de diámetro constante, mostrado en la Fig. 2-2. El flujo es turbulento por lo que podemos asumir condiciones de flujo en pistón, considerando cada porción de líquido pasando por la tubería como una unidad. No hay gradientes radiales de velocidad o de cualquier otra propiedad. Sin embargo, pueden existir gradientes axiales.
 |
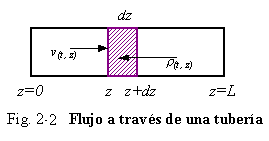La densidad y la velocidad pueden cambiar a medida que el fluido pasa a través de la dirección axial z. Ahora hay dos variables independientes: tiempo t y posición z. La densidad y velocidad son funciones de ambas variables t y z: r(t,z) y u (t,z). Nosotros queremos aplicar la ecuación total de continuidad [Ec. (2.1)] a un sistema de pequeñas partículas. El sistema es ahora “microscópico”. El elemento diferencial esta localizado en una longitud arbitraria z a lo largo de la tubería. Esta es dz y tiene un área igual a la sección transversal de la tubería A (pies3 o m3).
La velocidad de cambio de masa dentro del sistema es:
 |
Adz es el volumen del sistema; r es la densidad. Las unidades de esta ecuación son lbm /min. o kg/min.
La masa entrando al sistema a través de los alrededores en la distancia z:
u Ar (2.5)
Notar que las unidades son lbm/min = (pies/min)(pies2)( lbm/ pies3).
La masa saliendo del sistema a través de los alrededores en la distancia z + dz:
 |
La expresión anterior para el flujo a z + dz puede darse como una serie de expansión de Taylor de una función f(z) en los alrededores de z. El valor de la función a una distancia dz desde z es
 |
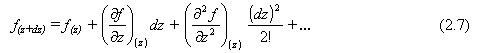Si la dz es pequeña, la serie puede ser truncada después del término de la primera derivada. Haciendo f(z) = u Ar dada por la Ec. (2.6).
Sustituyendo estos términos en la Ec. (2.1) da
 |
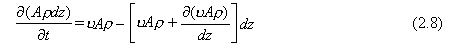Cancelando los términos dz y asumiendo que A es constante se tiene
 |
B. ECUACIÓN DE CONTINUIDAD POR COMPONENTE (BALANCES DE COMPONENTE).
Si ocurre una reacción dentro de un sistema, el número de moles de un componente individual se incrementará si es un producto de la reacción o disminuye si es un reactante, lo cual indica que la masa de una especie no que interviene en la reacción se conserva. Entonces la ecuación de continuidad de la j especie química del sistema será
Las unidades de esta ecuación son moles de componente j por unidad de tiempo.
Los flujos de entrada y salida pueden ser ya sea por convección (debido al flujo del “bulk”) y molecular (debido a la difusión). Se puede escribir una ecuación de continuidad para cada componente en el sistema. Si hay NC componentes, habrá NC ecuaciones de continuidad para componentes para el sistema. Sin embargo la única ecuación de balance total de masa y estos NC balances de componentes no son independientes, ya que la suma de todos los moles multiplicado por su respectivo peso molecular es igual al total de masa. Entonces un sistema dado tiene solamente NC ecuaciones de continuidad independientes. Nosotros generalmente en los cálculos usamos el balance total de masa y NC – 1 balances de componentes. Por ejemplo en un sistema binario (dos componentes), será un balance total y un balance de componente
Ejemplo 2.3. Considerar el mismo tanque de liquido perfectamente mezclado usado en el Ejemplo 2.1 excepto que una reacción química se lleva a cabo en el liquido dentro del tanque. El sistema es ahora un CSTR (reactor continuo tipo tanque agitado) como se muestra en la Fig. 2-3. El componente A reacciona irreversiblemente y a una velocidad especifica de reacción k forma el componente B.
 |
Denominando a la concentración de componente A en la alimentación al reactor como CAo (moles de A por unidad de volumen) y en el reactor CA. Asumiendo una reacción simple de primer orden, la velocidad de consumo de reactante A por unidad de volumen será directamente proporcional a la concentración instantánea de A dentro del tanque. En términos de la Ec. (2.9) para el balance del reactante A,
Flujo de A entrando al sistema = FoCAo
Flujo de A saliendo del sistema = FCA
Velocidad de formación de A por reacción = – VkCA
 |
El signo menos indica que A es consumiendo, y no producido. Las unidades de todos estos términos deben ser las mismas: moles de A por unidad de tiempo. Entonces el termino VkCA debe tener estas unidades, por ejemplo (pies3)(min–1)(moles de A/pies3). Luego las unidades de k en el sistema son min–1.
 |
Combinando con las anteriores se tiene
 |
Se ha usado una derivada ordinaria ya que t es la única variable independiente en este sistema. Las unidades de esta ecuación de continuidad de componente son moles de A por unidad de tiempo. El lado izquierdo de esta ecuación es el término dinámico. Los dos primeros términos del lado derecho son los términos convectivos. El ultimo término es el término generación.
Desde que el sistema es binario (componentes A y B), deberíamos escribir otra ecuación de continuidad por componente para B. Si CB es la concentración de B en moles de B por unidad de volumen.
 |
Notar el cambio de signo antes del término generación, lo cual indica que B esta siendo producido por la reacción. Alternativamente se puede usar la ecuación total de continuidad [Ec. (2.3)] donde CA , CB y r están relacionados por
MACA + MBCB = r (2.11)
Donde MA y MB son los pesos moleculares de los componentes A y B respectivamente.
Ejemplo 2.4. Supongamos que se tiene el mismo sistema macroscópico anterior excepto que ahora ocurre una reacción consecutiva. Reactante A se transforma en B a una velocidad de reacción específica k1, pero B puede reaccionar a una velocidad especifica de reacción k2 para formar un tercer componente C.
 |
Asumiendo reacción de primer orden, en términos de la Ec. (2.9), las ecuaciones de continuidad para los componentes A, B y C son
 |
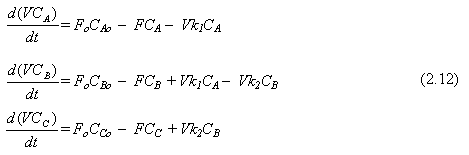Las concentraciones de los componentes se relacionan a la densidad, con (M = P.M.)
 |
Para cálculos se podrían usar estos tres balances por componente o dos de ellos y el balance total.
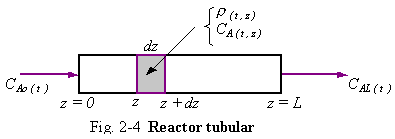
Ejemplo 2.5. Considerando el fluido pasando a través de una tubería como en el Ejemplo 2.2, suponer que la tubería es un reactor tubular en el cual se lleva a cabo la misma reacción del Ejemplo 2.3, A 
B cuando el material se mueve a lo largo del reactor la concentración de reactante CA disminuye a medida que A es consumido. La densidad r, velocidad u, y la concentración CA pueden variar con el tiempo y la posición axial z. Asumiendo condiciones de flujo en pistón de tal manera que no existan gradientes radiales en la velocidad, densidad o concentración.
La concentración de A alimentada a la entrada del reactor a z = 0 se define como
CA(t,0) = CA0(t) (2.14)
La concentración de A en el efluente del reactor a z = L se define como
CA(t,L) = CAL(t) (2.15)
Si queremos aplicar la ecuación de continuidad para el reactante A para un pequeño cilindro de longitud dz, como se muestra en la Fig. 2-4. los términos de entrada se pueden dividir en dos tipos: flujo de masa y difusión. La difusión puede ocurrir debido a la gradiente de concentración en la dirección axial. Esto es mucho menos importante que el flujo de masa en la mayoría de sistemas prácticos, pero esto lo incluimos aquí para ver cuanto contribuye al modelo. Podemos decir que la difusividad del flujo de A, NA (moles de A por unidad de tiempo por unidad de área), está dado por una relación tipo Ley de Ficks
 |
Donde DA es un coeficiente de difusión que abarca a la difusión y a la turbulencia de flujo del fluido. DA tiene unidades de longitud2 por unidad de tiempo.
Los términos en la ecuación general de continuidad de componente (Ec. 2.9) son: flujo molar de A dentro de los limites en la distancia z (flujo de masa y difusión)
= v ACA + ANA (moles de A/s)
 |
 |
2.4.2 Ecuación de Energía
La primera ley de la termodinámica lleva adelante el principio de conservación de energía. Escribiendo para un sistema abierto (donde puede ocurrir entrada y salida de flujo de material) esto es:
 |
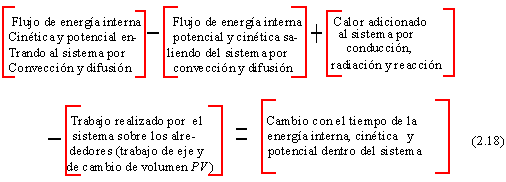Ejemplo 2.6. El CSTR del Ejemplo 2.3 será considerado nuevamente, esta vez con un dispositivo de enfriamiento dentro del tanque que puede remover el calor de la reacción exotérmica l (Btu/lb.mol de A reaccionado). Usamos la convención normal de que l es negativo para una reacción exotérmica y positivo para una reacción endotérmica. La razón de generación de calor (energía por unidad de tiempo) debido a la reacción es igual al consumo de A por l.
QG = – l VCA k (2.19)
 |
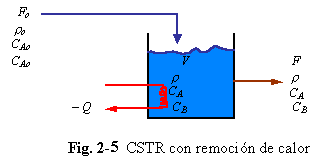La cantidad de calor removido desde la masa reaccionante por el medio de enfriamiento es –Q (energía por tiempo). La temperatura de la corriente de alimentación es To y la temperatura en el reactor es T (°R o K). Escribiendo la Ec. 2.18 para el sistema,
 |
donde U = energía interna (energía por unidad de masa)
K = energía cinética (energía por unidad de masa)
f = energía potencial (energía por unidad de masa)
W = trabajo de eje realizado por el sistema (energía por tiempo)
r = presión del sistema
Po = presión de la corriente de alimentación
Notar que todos los términos en la Ec (2.20) deben tener las mismas unidades (energía por tiempo), así los términos FP deben usar el factor de conversión apropiado (778 pies.lbf /Btu en el sistema inglés de unidades)
En el sistema mostrado en la Fig. 2-5 no se hace ningún trabajo de eje, así W = 0. Si las velocidades de flujo de entrada y salida no son muy altas, el término de energía cinética es despreciable. Si la elevación de los flujos de entrada y salida están mas o menos al mismo nivel, el término de energía potencial es pequeño. Entonces la Ec. 2.20 se reduce a:
 |
Donde 
es el volumen especifico (pies3/lbm 0 m3/kg), el reciproco de la densidad.
La entalpía H o h, se define:
H o h º U + P 
(2.22)
Nosotros usaremos h para la entalpía de una corriente liquida y H para la entalpía de una corriente de gas o vapor. Luego, para el CSTR, la Ec. (2.21) será
 |
Para líquidos en término P 
es despreciable comparado con el termino U, y podemos usar la velocidad de cambio de la entalpía del sistema en lugar de la energía interna del sistema
 |
Las entalpías son funciones de la composición, temperatura, y presión, pero principalmente de la temperatura. A partir de la termodinámica, la capacidad calorífica a presión constante, CP, y a volumen constante Cv, son:
 |
Para demostrar que la energía es primeramente influenciada por la temperatura, haremos una simplificación del problema asumiendo que la entalpía del liquido puede ser expresada como un producto de la temperatura absoluta y una capacidad calorífica promedio Cp, (Btu/lbm °R o cal/g K) que es constante.
H = Cp T
También asumiremos que las densidades de todas las corrientes liquidas son constantes. Con estas simplificaciones la Ec. 2.24 será
 |
Ejemplo 2.7. Para mostrar que forma toma la ecuación de energía para un sistema de dos fases, considerar el proceso en un CSTR mostrado en la Fig. 2-6. Dos corrientes de producto una liquida F y una vapor Fv (flujo volumétrico) son sacadas como corrientes laterales desde el recipiente. La presión en el reactor es P. Los volúmenes de vapor y liquido son Vv y V. La densidad y temperatura de la fase vapor son r v y Tv. La fracción molar de A en el vapor es y. Si las fases están en equilibrio térmico, las temperaturas del vapor y el liquido son iguales (T = Tv). Si las fases están en equilibrio de fases, las composiciones del vapor y el liquido están relacionadas por la ley de Raoult, una relación de volatilidad relativa o alguna otra relación de equilibrio liquido-vapor.
 |
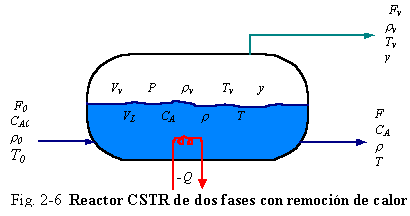La entalpía de la fase vapor H (Btu/lbm o cal/g) es una función de la composición y, temperatura Tv, y presión P. Despreciando los términos de energía cinética, energía potencial y trabajo, y relacionando las energías internas con las entalpías en la derivada con respecto al tiempo, la ecuación de energía del sistema (contenido de vapor y liquido en el tanque) será:
 |
En orden a expresar esta ecuación explícitamente en términos de temperatura, usamos una forma muy simple para h (h = CPT) y una forma igualmente simple para H.
H = CP T + l v (2.28)
Donde l v es un calor de vaporización promedio de la mezcla. En un modelo más riguroso l v podría ser una función de la temperatura T v, composición y, y presión P. La ecuación (2.27) estará dada por:
Ejemplo 2.8. Para ilustrar la aplicación de la ecuación de energía a un sistema microscópico, retornando al reactor tubular de flujo en pistón y ahora teniendo un cambio de temperatura a medida que el fluido pasa a través de la tubería. Nuevamente asumimos que no hay gradiente radial de velocidad, concentración, o temperatura (esta no es una asunción consistente si el diámetro de la tubería es grande y el sistema es altamente exotérmico). Suponemos que el reactor tiene una chaqueta de enfriamiento como se muestra en la Fig. 2-7. El calor puede ser transferido desde el fluido de proceso a temperatura T hacia la pared metálica del reactor a temperatura TM.
 |
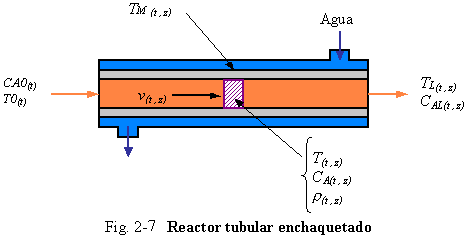El calor es subsecuentemente transferido hacia el agua de enfriamiento. Para una descripción completa del sistema podríamos necesitar ecuaciones de energía para el fluido de proceso, pared metálica, y el agua de enfriamiento. Aquí solamente analizaremos lo concerniente al fluido de proceso.
Tomando una pequeña porción de fluido como el sistema, podemos derivar cada uno de los términos de la Ec. (2.18). los términos de energía potencial y cinética se asumen despreciables, así como el trabajo. Se asumen las formas simplificadas de la energía interna y de la entalpía. Se asume despreciable el flujo por difusión comparado al flujo del “bulk”. Incluimos la posibilidad de la conducción de calor axial a lo largo del reactor debido a las condiciones moleculares o de turbulencia
Flujo de energía (entalpía) entrando a la distancia z debido al flujo de masa:
nAr CPT con unidades inglesas de ingeniería de
 |
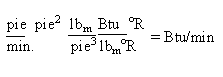Flujo de energía (entalpía) saliendo a la distancia z + dz:
 |
Calor generado por reacción química = – A dz kCA l
Calor transferido a la pared del metal = – hT(pD dz) (T – TS)
donde hT = coeficiente de película, Btu/min pie2 °R
D = diámetro de tubería, pies
Conducción de calor hacia los alrededores a z = qs A
donde qs es el flujo de calor en la dirección z debido a la conducción. Usando la Ley de Fourier para expresar qs en términos de la temperatura como fuerza impulsora:
 |
donde kT es una conductividad térmica efectiva, con unidades Inglesas de ingeniería de Btu/pie.min.°R.
 |
Combinando todos estas ecuaciones se tiene:
 |
2.4.3 Ecuación de Movimiento
La segunda Ley de movimiento de Newton dice que la fuerza es igual al producto de la masa por la aceleración para un sistema de masa constante M.
 |
donde F = fuerza, N (lbf)
m = masa, Kg. (lbm)
gc = constante de conversión necesaria cuando se usan unidades Inglesas de
ingeniería, para mantener consistencia en las unidades = 32,2 lbm pie/lbf seg2
Esta es la relación básica, la cual es usada para la ecuación de movimiento para un sistema. En una forma más general, donde la masa puede variar con el tiempo,
 |
donde vi = velocidad en la dirección i, m/s (pies/s)
Fji = j-ésima fuerza actuando en la dirección i
La Ec. (2.33) dice que la velocidad de cambio de momentum en la dirección i (masa por velocidad en la dirección i) es igual a la suma neta de las fuerzas actuando en la dirección i. Esto puede establecerse como un balance dinámico de fuerzas. O más elocuentemente esto es denominado la conservación de momentum.
En el mundo real existen tres direcciones: x, y, z. Entonces para cualquier sistema se pueden escribir tres balances de fuerzas. Por lo tanto, cada sistema tiene tres ecuaciones de movimiento (además de una para el balance total de masa, una ecuación de energía, y NC – 1 balances de componentes).
En lugar de escribir tres ecuaciones de movimiento, es a menudo más conveniente (y siempre más elegante) escribir las tres ecuaciones como un vector. Nosotros no usaremos la forma vectorial en este libro ya que todos nuestros ejemplos serán simples con balances de fuerzas en una dirección. Los tratados de mecánica de fluidos hacen uso extensivo de la conservación de momentum.
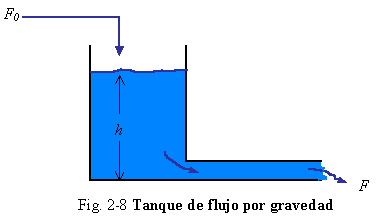
Ejemplo 2.9. El flujo por gravedad del tanque mostrado en el Cap. 1, proporciona un ejemplo simple de la aplicación de la ecuación de movimiento para un sistema macroscópico. Refriéndonos a la Fig. 2-8 consideramos que la longitud de la línea de salida sea L m (pies) y su área de sección transversal Ap m2 (pies2). El tanque cilíndrico vertical tiene un área de sección transversal de AT m2 (pies2).
La parte de este proceso que es descrita por un balance de fuerzas es el liquido fluyendo a través de la tubería. Este tendrá una masa igual al producto del volumen de la tubería (ApL) por la densidad del liquido r. Esta masa de liquido tendrá una velocidad v m/s (pies/s) igual al flujo volumétrico dividido por el área de sección transversal de la tubería. Recordar que hemos asumido condiciones de flujo en pistón y de liquido incompresible, y por lo tanto todo el liquido se está moviendo a la misma velocidad, mas o menos similar a una varilla sólida. Si el flujo es turbulento esta no es una mala asunción.
 |
 |
La cantidad de liquido en la tubería no cambiará con el tiempo, pero si queremos cambiar la cantidad de flujo de salida, debe ser cambiada la velocidad del liquido. Y para cambiar la velocidad o el momentum del liquido, debemos ejercer una fuerza sobre el liquido.
La dirección de interés en este problema es la horizontal, ya que se asume que la tubería es horizontal. La fuerza actuando sobre el liquido en el extremo izquierdo de la tubería es la fuerza de presión hidráulica del liquido en el tanque
 |
Las unidades de esta fuerza son N (lbf)
La presión estática en el tanque y al final de la tubería es la misma.
La única fuerza actuando en dirección opuesta, de derecha a izquierda y oponiéndose al flujo es la fuerza de fricción debido a la viscosidad del liquido. Si el flujo es turbulento, la fuerza de fricción será proporcional al cuadrado de la velocidad y la longitud de la tubería.
Fuerza de fricción = KF L v2 (2.36)
Reemplazando esta fuerza en la Ec. 2.32 tenemos
 |
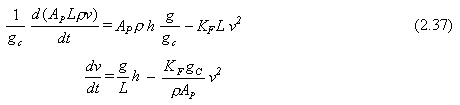El signo de la fuerza de fricción es negativo debido a que actúa en la dirección opuesta al flujo. Hemos definido de izquierda a derecha la dirección positiva.
Ejemplo 2.10. Probablemente el mejor ejemplo contemporáneo de un sistema de masa variable podría ser la ecuación de movimiento para un cohete espacial en el cual la masa decrece a medida que se consume el combustible. Sin embargo en concordancia con los sistemas de ingeniería química, consideraremos el problema mostrado en la Fig. 2-9. Las tuberías de petróleo son algunas veces usadas para transportar diferentes productos desde una localidad a otra sobre una base por lotes, por así decirlo, un producto por vez. Para reducir la contaminación, al final del transporte de cada lote, una bola limpiadora “pig” que cabe justo en la tubería, es insertada en un extremo de la línea. Luego se introduce gas inerte para hacer que la bola vaya hacia el otro extremo, en cuyo recorrido se produce la limpieza de la línea de cualquier liquido que hubiese quedado en ella.
Para escribir un balance de fuerzas para el liquido en la tubería a medida que es evacuado hacia fuera, debemos tomar en cuenta el cambio de masa del material. Asumiendo que el peso y la fricción de la bola es despreciable comparada con el liquido en la línea. Tomando como z la posición axial de la bola en cualquier tiempo. El liquido es incompresible (densidad r) y fluye en flujo en pistón. Esto produce una fuerza de fricción proporcional al cuadrado de su velocidad y a la longitud de la tubería conteniendo liquido.
Fuerza de fricción = KF(L – z)v2 (2.38)
 |
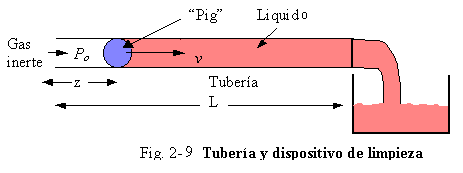El área de sección transversal de la tubería es AP. La masa de fluido en la tubería es (L – z)APr
La presión P0 (lbf/pie2 manométrica) de gas inerte presionando al dispositivo de limpieza es esencialmente constante a lo largo de toda la tubería. El tanque en el cual se recoge el liquido está a presión atmosférica. La tubería es horizontal. Un balance de fuerzas en la dirección horizontal z dará:
 |
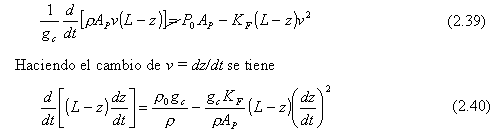Ejemplo 2.11. Como un ejemplo de un balance de fuerzas para un sistema microscópico, tomaremos el problema clásico del flujo laminar de un fluido newtoniano incompresible en una tubería cilíndrica. Por “newtoniano” se define que su esfuerzo cortante es proporcional al esfuerzo de velocidad o gradiente de velocidad.
 |
donde trz = esfuerzo de velocidad (esfuerzo cortante por unidad de área) actuando en la dirección z y perpendicular al eje r, lbf/pie2.
vz = velocidad en la dirección z, pies/s
= gradiente de velocidad de vz en la dirección r
m = viscosidad del fluido, lbm/pie .s
En muchas industrias, la viscosidad es reportada en centipoises o poises. El factor de conversión es 6,72 x 10-4 (lbm/pie .s)/centipoise.
Considerando nuestro sistema como un pequeño elemento del fluido, el cual es mostrado en la Fig. 2-10. Desde que el fluido es incompresible, no existe flujo radial del fluido, o vr = 0. El sistema es simétrico con respecto a la coordenada angular (alrededor de la circunferencia de la tubería), y entonces debemos considerar solamente las dos dimensiones r y z. Las fuerzas en la dirección z actuando sobre el elemento son:
Fuerzas actuando de izquierda a derecha:
 |
Fig. 2-10 Flujo laminar en una tubería
El término dP/dz, o la caída de presión por pie de tubería, será constante si el fluido es incompresible. Esté término se denominará D P/L. Reemplazando la Ec. (2.41) en la Ec. (2.44) da
2.4.4 Ecuaciones de transporte
Nosotros hemos venido usando en los ejemplos la mayoría de leyes que gobiernan la transferencia de energía, masa y momentum. Estas leyes de transporte, todas tiene la forma de un flujo (velocidad de transferencia por unidad de área) siendo proporcional a la fuerza impulsora (o gradiente de la temperatura, concentración, o velocidad). La constante de proporcionalidad es una propiedad física del sistema (tal como conductividad térmica, difusividad o viscosidad).
Para transporte en un nivel molecular, las leyes toman los nombres familiares de Fourier, Ficks y Newton.
Las relaciones de transferencia de una forma macroscópica más amplia también son usadas; por ejemplo coeficiente de película y coeficiente total en transferencia de calor. Aquí, la diferencia en las propiedades del “bulk” entre dos puntos es la fuerza impulsora. La constante de proporcionalidad es un coeficiente total de transferencia. La Tabla 2.3 resume algunas de las diferentes relaciones usadas en el desarrollo de los modelos.
Tabla 2.3 Leyes de transporte
| Cantidad | Calor | Masa | Momentum |
| Flujo | q | NA | trz |
| Transporte molecular | |||
| Fuerza impulsora |  |
 |
 |
| Leyes | Fourier | Fick | Newton |
| Propiedad | Conductividad térmica
kT |
Difusividad
ÒA |
Viscosidad
m |
| Transporte total | |||
| Fuerza impulsora | D T | D CA * | D P |
| Relaciones | q = hT D T | NA = kLD CA | ** |
* Fuerza impulsora en términos de presión parcial y fracción molar también es comúnmente usada.
** El problema más común es determinar la caída de presión a través de tuberías, usando las
correlaciones para el factor de fricción f = (gC D DP/ L)/ 2r v2.
2.4.5 Ecuaciones de estado
Para escribir modelos matemáticos son necesarias ecuaciones que describan las propiedades físicas, principalmente la densidad y entalpía, como funciones de la temperatura, presión y composición.
Densidad del liquido = r L = f(P, T, x)
Densidad del vapor = r v = f(P, T, x) (2.46)
Entalpía del liquido = h = f(P, T, x)
Entalpía del vapor = H = f(P, T, x)
Ocasionalmente estas relaciones tienden a ser muy complejas para describir los sistemas con exactitud. Pero en muchos casos se pueden hacer simplificaciones sin sacrificar mucha exactitud. Algunas ecuaciones simples de la entalpía usadas en los ejemplos de balance de energía son:
h = CP T (2.47)
H = CP T + l v
El siguiente nivel de complejidad podría ser si se hacen los CP’s funciones de la temperatura:
 |
Con frecuencia se usa para CP un polinomio en T
CP(T) = A1 + A2 (2.49)
Luego la Ec. (2.48) será:
 |
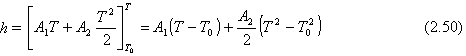Desde luego, con mezclas de componentes es necesaria la entalpía total. Si los efectos de calor de mezcla son despreciables, pueden promediarse las entalpías de los componentes puros:
 |
donde xj = fracción molar del componente j
Mj = peso molecular del componente j
hj = entalpía del componente puro j, energía por unidad de masa
El denominador de la Ec. (2.51) es el peso molecular promedio de la mezcla.
Las densidades de los líquidos, se pueden asumir como constantes en muchos sistemas, siempre que no ocurran grandes cambios en la temperatura y composición. Las densidades del vapor usualmente no pueden ser consideradas invariantes y a menudo son necesarias relaciones PVT. La relación más simple y más usada es la ley del gas perfecto:
PV = nRT (2.52)
donde P = presión absoluta (lbf/pie2 o kiloPascales)
V = volumen (pies3 o m3)
n = número de moles (lb.mol o kg.mol)
R = constante = 1545 lbf pie/lb.mol °R o 8,314 kPa m3/kg.mol K
T = temperatura absoluta (°R o K)
Rearreglando para obtener una ecuación para la densidad rv (lbm/pie3 o kg/m3) de un gas perfecto con un peso molecular M, se tiene
 |
2.4.6 Equilibrio
La segunda ley de la termodinámica es la base para las ecuaciones que describen las condiciones de un sistema cuando prevalecen las condiciones de equilibrio.
A. EQUILIBRIO QUÍMICO. El equilibrio en un sistema reaccionante ocurre cuando:
 |
donde vj = coeficiente estequiométrico del componente j teniendo signo negativo los reactantes y signo positivo los productos
m i = potencial químico del componente
El camino usual para trabajar con esta ecuación es en términos de una constante de equilibrio para una reacción. Por ejemplo, considerar una reacción reversible en fase gas de A para formar B a una velocidad específica k1 y B reaccionando para convertirse en A a una velocidad de reacción específica k2. La estequiometría de la reacción es tal que va moles de A reaccionan para formar vb moles de B.
 |
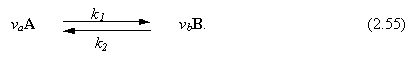La Ec. (2.54) dice que el equilibrio ocurre cuando
vb mB – va ma = 0 (2.56)
El potencial químico para una mezcla perfecta de gases se puede escribir
mj = 
+ RT ln Pj (2.57)
donde 
= potencial químico estándar (o energía libre de Gibbs por mol) del
componente j, la cual es una función de la temperatura solamente
R = constante del gas perfecto
T = temperatura absoluta
Pj = presión parcial del componente j
Sustituyendo en la Ec. (2.56)
 |
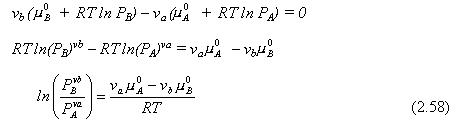El lado derecho de esta ecuación es una función de la temperatura solamente. El término en paréntesis en el lado izquierdo es definido como la constante de equilibrio KP, y describe las razones de equilibrio de productos y reactantes.
 |
B. EQUILIBRIO DE FASES. El equilibrio entre dos fases ocurre cuando el potencial químico de cada componente es el mismo en las dos fases
(2.60)
donde 
= potencial químico de la especie j en la fase I
= potencial químico de la especie j en la fase II
Debido a que la gran mayoría de sistemas químicos involucran fases de liquido y vapor, se usan muchas relaciones de equilibrio liquido – vapor. En el rango desde los muy simples a los muy complejos. Algunas de las relaciones más comúnmente usadas son listadas a continuación. Tratados con mayor detalle son presentados en los textos de termodinámica. Algunos de los conceptos básicos son introducidos por Luyben y Wenzel en “Chemical Process Analysis: Mas and Energy Balances”, Chaps, 6 y 7, Prentice Hall, 1988.
Básicamente nosotros necesitamos una relación que nos permita la composición del vapor si conocemos la composición del liquido o viceversa. El problema más común es un calculo de punto de burbuja: calcular la temperatura T y la composición del vapor yj, dada la presión P y la composición del liquido xj. Esto usualmente involucra un calculo de prueba y error, en solución iterativa debido a que las ecuaciones pueden ser resueltas explícitamente solamente en los casos simples. Algunas veces se tienen cálculos de punto de burbuja que se inician en valores conocidos de xj y T, y se deben encontrar P e yj. Esto es usualmente más fácil que cuando la presión es conocida debido a que los cálculos de punto de burbuja usualmente no son iterativos.
Los cálculos de punto de rocío se pueden hacer cuando se conoce la composición del vapor yj y P (o T) y se quiere encontrar la composición del liquido xj (o P), los cálculos para evaporación “flash” se deben hacer cuando se conocen ya sea xj o yj y deben combinarse las relaciones de equilibrio de fases, ecuaciones de balance de componentes, y un balance de energía para encontrar el resto de incógnitas.
Nosotros asumiremos comportamiento ideal de la fase vapor en los ejemplos, por ejemplo, la presión parcial del componente j en el vapor es igual al producto de la presión total P por la fracción molar del componente j en la fase vapor yj (Ley de Dalton).
Pi = Pyi (2.61)
Se pueden requerir correcciones para altas presiones
En la fase vapor se han usado extensamente varias aproximaciones,
1. Ley de Raoult.- Los líquidos que obedecen la Ley de Raoult son denominados ideales
 |
donde 
es la presión de vapor del componente puro j. Las presiones de vapor son funciones de la temperatura solamente. Esta dependencia es a menudo descrita por
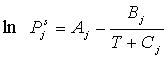(2.64)
2. Volatilidad relativa.- La volatilidad relativa aij del componente i con respecto al componente j se define por:
 |
La volatilidad relativa tiende a ser constante para un gran número de sistemas. Por conveniencia es frecuente mente usada así.
En un sistema binario la volatilidad relativa a del componente más volátil comparado con el componente menos volátil es
 |
3. Valores K.- Se usan extensamente las razones de vaporización o valores K, particularmente en la industria del petróleo
 |
Los valores K son funciones de la temperatura y composición, y en menor extensión de la presión.
4. Coeficientes de actividad.- Para líquidos no ideales la Ley de Raoult debe ser modificada para compensar la no-idealidad en la fase liquida. Los “factores de desviación” usados son denominados coeficientes de actividad.
 |
Donde gj es el coeficiente de actividad para el componente j. El coeficiente de actividad es igual a 1 si el componente es ideal. Los g ’s son funciones de la composición y temperatura.
2.4.7 Cinética Química
Los ingenieros químicos deben modelar muchos reactores químicos, y deben estar familiarizados con las relaciones básicas y terminología usadas en la descripción de la cinética (velocidad de reacción) de reacciones químicas.
A. DEPENDENCIA DE LA TEMPERATURA (LEY DE ARRHENIUS). El efecto de la temperatura sobre la velocidad específica de reacción k es usualmente encontrada a ser exponencial:
k = a 
(2.69)
donde k = velocidad específica de reacción
a = factor pre-exponencial
E = energía de activación: muestra la dependencia de la velocidad de reacción con la temperatura, así, para un valor E grande, es rápido el incremento de k con el incremento de la temperatura, (Btu/lb . mol o cal/g. mol)
T = temperatura absoluta
R = constante del gas perfecto = 1,99 Btu/lb . mol °R o 1,99 cal/g . mol K
Esta dependencia exponencial de la temperatura representa una de las más severas no linealidades en sistemas de ingeniería química. Se debe tener presente que la dependencia “aparente” de una reacción con respecto a la temperatura puede no ser exponencial si la reacción es limitada por la transferencia de masa, y no limitada por la reacción química. Si en la operación de un reactor están presentes las dos zonas, obviamente el modelo matemático deberá incluir los efectos de la velocidad de reacción y transferencia de masa.
B. LEY DE ACCIÓN DE LAS MASAS. Usando la notación convencional definimos la velocidad global de reacción  como la velocidad de cambio de los moles de cualquier componente por unidad de volumen, debido a la reacción química dividido por su coeficiente estequiométrico.
 |
Los coeficientes estequiométricos vj son positivos para los productos de la reacción y negativos para los reactantes. Notar que  es una propiedad intensiva y puede ser aplicada a sistemas de cualquier tamaño.
Por ejemplo, para la reacción en la cual reaccionan A y B para formar C y D
| va A + vb B |  |
vc C + vd D |
Luego
 |
La ley de acción de las masas dice que la velocidad de reacción total  variará con la temperatura (debido a que k es dependiente de la temperatura) y con la concentración de reactantes elevada a alguna potencia.
 = k(T) (CA)a (CB)b (2.72)
donde CA = concentración del componente A
CB = concentración del componente B
Las constantes a y b, en general no son iguales a los coeficientes estequiométricos va y vb. La reacción se denomina de primer orden en A si a = 1. Es de segundo orden en A si a = 2. Las constantes a y b pueden ser fracciones.
Como se ha indicado claramente, las unidades de la velocidad de reacción específica dependen del orden de reacción. Esto se debe a que la velocidad de reacción total  siempre tiene las mismas unidades (moles por unidad de tiempo por unidad de volumen). Para una reacción de primer orden de A reaccionando para dar B, la velocidad de reacción total Â, escrita para el componente A, podría tener las unidades de moles de A/min pie3.
 = k CA
Si CA tiene las unidades de moles de A/pie3, k debe tener las unidades de min-1.
Si la velocidad de reacción total para el sistema anterior es de segundo orden en A,
 = k 
 mantiene las unidades de moles de A/min pie3. Entonces k debe tener las unidades de pies3/min mol de A.
Considerando la reacción A + B ——–> C. Si la velocidad de reacción total es de primer orden con respecto a A y con respecto a B
 = k CACB
 mantiene las unidades de moles de A/min pie3. Entonces k debe tener las unidades de pies3/min mol de B.
2.5 MODELIZACIÓN EN BASE A DATOS EXPERIMENTALES
Es frecuente el problema de tener un conjunto de mediciones y desear ajustar los datos observados a funciones que describan la relación entre la variable dependiente y la variable independiente. El problema original parece estar asociado al nombre de Gauss quien trató de ajustar curvas a datos experimentales obtenidos en observaciones astronómicas. En nuestros días el planteamiento permite establecer un modelo matemático basado en optimización, para dar solución al problema de calcular los coeficientes que satisfacen el criterio de mínimos cuadrados. En el presente capítulo mostraremos de forma sencilla la solución matricial del problema, ilustrando la forma de llegar a una expresión cerrada de la solución. Con ejemplos sencillos se tiene una comprobación al aplicar en forma directa la solución presentada.
2.5.1 DESARROLLO DE ECUACIONES PARA EL CÁLCULO DE LOS COEFICIENTES
Con el fin de establecer la nomenclatura general se considera que se tiene un conjunto de n pares de observaciones (xi, yi). En un plano x-y se puede visualizar la distribución de observaciones usando un diagrama de dispersión, Fig. 2.11.
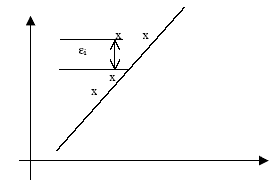
Fig. 2.11. Diagrama de dispersión, observaciones en el plano x-y.
Como se muestra en la figura 1, para cada observación se tiene un valor teórico expresado por la ecuación de la función. Así, se puede hablar de un error o “desajuste” a la diferencia entre el valor observado y el valor teórico. Al sumar los errores al cuadrado, se tiene SS.
En el caso particular cuando los datos pueden ser descritos por una recta,
y = a1x + ao,
se requieren los coeficientes a1 y ao. Los mejores coeficientes serán aquellos que minimizan el cuadrado de los errores, dando lugar al método de mínimos cuadrados. El gradiente de SS igualado a cero será la solución buscada. De la figura 2.11:
Para el caso particular de n = 4 observaciones, la suma SS del cuadrado de los errores:
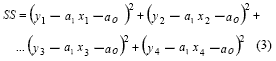
El gradiente de SS:
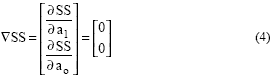
y las componentes del gradiente (4) se obtienen como:
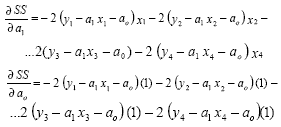
Al igualar a cero las componentes del gradiente y en forma matricial:
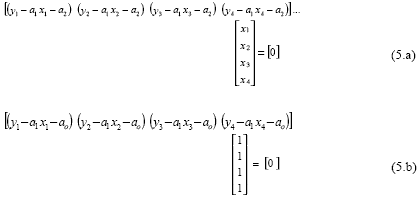
Las formas anteriores (5.a) y (5.b) se pueden escribir en una sola expresión matricial:
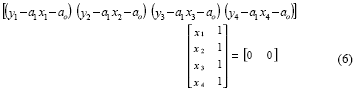
y al transponer (6):
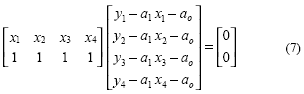
Se puede arreglar (7) y obtener una forma condensada de la solución para a1 y ao.
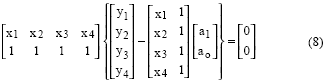
Llamando A a la matriz que tiene la información de la medición en variable independiente x, como At a la matriz que presenta en forma de renglones las columnas de A y al vector de información de
medición en la variable dependiente y, se tiene:
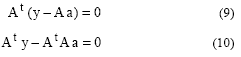
con solución:
La dimensión de A depende de n número de observaciones y del número de coeficientes a determinar.
Ejemplo 2.12
Para ilustrar la aplicación de (11) se propone los siguientes pares de valores medidos, para la variable independiente x y el correspondiente valor de la variable dependiente y.
Los arreglos de información, para n = 4:
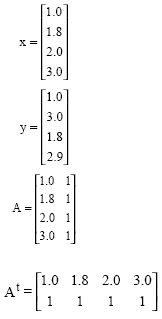
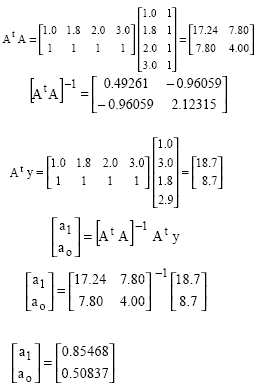
Con solución para los coeficientes a1 y ao, que resultan en la recta y = 0.85468 x + 0.50837. Una gráfica de la recta ajustada y de los valores observados se muestra en la figura 2.12.
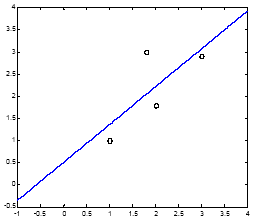
Fig. 2.12. Gráfica de función ajustada y = 0.85468 x + 0.50837 y las mediciones.
2.6 MODELOS DE POBLACIÓN
2.6.1 Patrones Elementales de Comportamiento de Sistemas Dinámicos
Los cinco patrones elementales de comportamiento de sistemas, los cuales a la vez son la descripción de un amplio conjunto de fenómenos ambientales son:
- El crecimiento (o la descomposición) lineal
- El crecimiento (o la descomposición) exponencial
- El crecimiento logístico
- Sobre paso (sobreimpulso) y colapso
- La oscilación.
Crecimiento (o descomposición) Lineal. Un ejemplo podría ser el consumo individual de comida en una expedición larga a bordo de barco (donde el suministro de comida se fija en algún valor inicial, y la comida adicional de fuentes exteriores no está disponible). Asumiendo que un individuo come una cantidad constante de comida cada día, podríamos modelar la cantidad de comida en las provisiones para la marina como:
Dónde hemos tomado la tasa constante de consumo, k, a ser positiva, y explícitamente hemos incluido el signo menos para indicar que A(t) disminuciones con el tiempo.
La solución a esta ecuación diferencial es:
Crecimiento (o la descomposición) exponencial. La población es el ejemplo fácil aquí. El crecimiento exponencial es caracterizado por la tasa de cambio, la cual es proporcional a la cantidad. Por lo tanto,
donde r es la tasa de crecimiento neta (el índice de natalidad menos la tasa de mortalidad).
La solución a esta EDO es:
Este modelo es el visualmente idéntico para un crecimiento super o subexponencial:
Donde q es típicamente una cantidad pequeña.
Sin embargo, desde que el crecimiento super-exponencial tiende a una cantidad infinita en una cantidad finita de tiempo, este modelo se usa en la investigación. Por ejemplo, el consumo mundial de petróleo de 1900 para 1970 fue mejor representado por una curva super-exponencial. ¡Como lo fue la población mundial de 1900 para 1990!
El Crecimiento logístico. Ningún estudio de crecimiento demográfico exponencial es completo sin incluir el concepto de capacidad de acarreo. Esto introduce una no-linealidad en la EDO lineal citada anteriormente. La forma más común para introducir la capacidad de acarreo es como sigue:
donde K es llamada la capacidad de acarreo (capacidad de carga del medio ambiente)
La solución, la cuál puede ser obtenida en forma analítica cerrada, es la característica curva-S estudiada en la biología demográfica y temas afines, cuyo número de aplicaciones es tremendo; ¡Podríamos gastar la mitad de año en estos temas aisladamente!
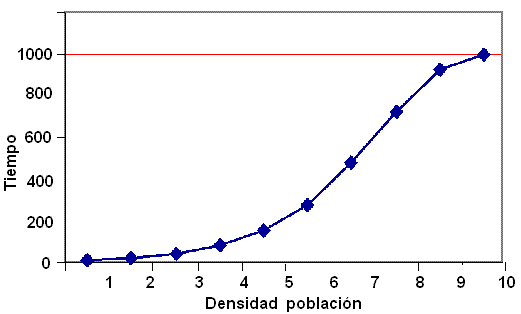
Sobreimpulso y colapso. Cuando una población es parcialmente o completamente dependiente de un recurso no renovable, el potencial existe para un colapso catastrófico de la población a medida que el consumo del recurso finito aumente. Esto podría ser modelado por el siguiente sistema:
donde b es el índice de natalidad percapita, R(t) la cantidad del recurso en el tiempo t, y R(0) la cantidad inicial de recuro.
donde c es la tasa de consumo per cápita, y N(t) es la población en el tiempo t.
Hay variaciones múltiples de este modelo, pero pero todos ellos permiten una solución donde la población crece rápidamente al principio, alcanza el máximo, y cae rápidamente para establecerse muy cerca a cero.
Soluciones Oscilatorias. Ciertamente estudiando el oscilador armónico simple se puede entender las EDO, la clase de sistemas dinámicos. Sin embargo, ilustraremos un conjunto diferente de dos EDO de primer orden acopladas, que describen la relación depredador-presa. Los ecologistas inician con las clásicas ecuaciones de Lotka-Volterra:
donde r es la tasa de crecimiento neta inherente, y a el coeficiente de predación para los especies de la víctima.
donde d es la tasa de mortalidad inherente para el depredador, y ß es coeficiente de predación para los especies del depredador.
La solución a este conjunto de ecuaciones da la clásica oscilación de Lotka-Volterra de cada especie. El diagrama de plano de fase de este modelo es una figura cerrada, pero añadiendo una sucesión de términos biológicamente más realistas al modelo resulta en una tipología matemática de atractores de plano de fase.
Estos cinco patrones de conducta básicos comprenden los tipos de respuestas que la mayoría de modelos ambientales complicados pueden producir.