LA FUNCIÓN DE TRANSFERENCIA - Ingeniería Química .tech

Nuestro principal uso de la s transformaciones da Laplace en control de procesos involucra la representación de la dinámica del proceso en términos de “Funciones de Transferencia”. Estas son relaciones salida-entrada y se obtienen mediante la transformada de Laplace de ecuaciones algebraicas y diferenciales.

Al examinar la Fig. 2.5, se plantea inmediatamente la posible relación existente entre las variables de entrada y las de salida. Al cociente entre las expresiones matemáticas de las variables de salida y de entrada en función del tiempo se le denomina función de transferencia o transmitancia y se representa por el símbolo G(p) o G(s), que recibe también el nombre de transmitancia isomorfa.

Para determinar la función de transferencia, consideremos un caso general en el cual las señales de entrada y salida de un sistema se expresarán mediante ecuaciones diferenciales lineales (una ecuación diferencial lineal es la formada por la suma de términos lineales, es decir por la suma de términos que son de primer grado con relación a las variables independientes).

donde ai y bi = coeficientes constantes

r = entrada o fuerza impulsora

y = salida

Representando la función derivada por el operador p = d/dt resulta:

(a_npⁿ+ a_(n-1)p^n-1 + …+ a₀)y = (b_mp^m + b_(m-1)p^m-1 + … + b₀)r (6.2)

y de aquí

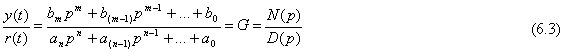
que es la relación entre las señales de salida y(t) y entrada r(t), ambas como funciones del tiempo. Esta relación recibe el nombre de función de transferencia del sistema.

En la expresión anterior, N(p) representa el numerador de la función de transferencia y D(p) representa el denominador, ambos en función del operador p. En caso de que la señal de entrada o de excitación del sistema sea nula, r(t) = 0 y el sistema evoluciona libremente de acuerdo con la expresión siguiente

D(p) = a_npⁿ + a_(n-1) p^n-1 + … + a₀ = 0 (6.4)

que se llama ecuación característica y cuyas raíces son p₁, p₂, p₃, … p_i y se denominan polos de la función de transferencia. Las raíces del numerador N(p) igualado a cero se denominan ceros de la función de transferencia.

De este modo, la ecuación característica puede expresarse como

a_n(p – p₁) (p – p₂) … (p – p_i ) (p – p_n) = 0 (6.5)

o bien, siendo en general p_í raíces imaginarias, la expresión anterior pasa a ser

D(p) = y(t) = c₁e^pt + c₂e^pt + … + c_ie^pt + … + c_n e^pt = 0 (6.6)

Para que el sistema sea estable, la curva y(t) debe ser de evolución amortiguada al crecer el tiempo, y por tanto las raíces p_i deben tener su parte real negativa, ya que entonces el término general c_ie^pt = c_ie^{(-r + ji)t} —–> 0 en el tiempo. Esta es una de las condiciones de estabilidad que se verá más adelante

Consideramos de nuevo la Ec. (6.1) como ecuación diferencial lineal que relaciona las señales de entrada y de salida a un sistema definido por la función de transferencia G.

Aplicando la transformada de Laplace a los dos miembros y considerando valores iniciales nulos en la función y en las derivadas resulta:

a_nsⁿY + a_(n-1)s^{n – 1}Y + . . . + a₀Y = b_ms^mR + b_(m–₁₎s^{m – 1}R + . . . + b₀R (6.7)

y de aquí

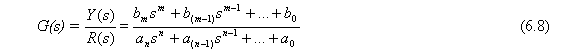
expresión equivalente a la Ec. (6.3) sin más que cambiar el operador diferencial p en el dominio del tiempo por la variable compleja s en el dominio de las s. Así pues, al ser las dos expresiones equivalentes, la función de transferencia se puede expresar también por el cociente de las transformadas de Laplace, siempre que se mantengan nulas las condiciones iniciales en la variable y sus derivadas. Utilizando este concepto de función de transferencia, se puede representar la dinámica de un sistema por ecuaciones algebraicas en s. Si la potencia más alta de s en el denominador de la función de transferencia es igual a n, se dice que el sistema es de orden n.

El valor de la salida se obtiene multiplicando la entrada por la función de transferencia.

6.1 ELEMENTOS DE LA FUNCIÓN DE TRANSFERENCIA

Para una ecuación que describe un sistema físico real Ec.(6.1), el orden del lado derecho, m, no puede ser mayor que el orden del lado izquierdo, n. Este criterio para una realizabilidad física es:

n ³ m (6.9)

Esta condición puede ser determinada intuitivamente por el siguiente razonamiento. Tomando un caso donde m = 1 y n = 0.

Esta ecuación dice que tenemos un proceso cuya salida y depende del valor de la entrada r y el valor de la derivada de la entrada. Entonces el proceso debe ser capaz de diferenciar, perfectamente, la señal de entrada. Pero es imposible para todo sistema real diferenciar perfectamente. Esto tomaría que un cambio de escalón en la entrada produzca una punta infinita en la salida. Esto es físicamente imposible.

Este ejemplo puede ser generalizado a cualquier caso donde m ³ n para mostrar que diferenciación debe requerir. Por lo tanto, n siempre debe ser mayor o igual a m. La transformada de Laplace de la Ec. (6.10) da:

Este es un adelanto de primer orden. Esto no es físicamente realizable; es decir, un dispositivo no puede ser construido que tenga exactamente esta función de transferencia

Considerar el caso donde n = m = 1.

Esto aparece que una derivada de la entrada es nuevamente requerida. Pero la Ec. (6.12) puede ser arreglada agrupando los términos de derivada juntos:

El lado derecho de esta ecuación contiene funciones del tiempo pero no derivadas. Esta EDO puede ser integrada mediante la evaluación del lado derecho (la derivada) en cada punto en el tiempo e integrando para conseguir z en el nuevo punto en el tiempo. Entonces, el nuevo valor de y es calculado a partir del valor conocido de r:

y = (z + b₁ r)/a₁ (6.14)

No se requiere diferenciación y esta función de transferencia es físicamente realizable.

Recordar, la naturaleza siempre integra. Nunca diferencia!

La transformada de Laplace de la Ec. (6.13) da la función de transferencia salida/entrada

Este es llamado un elemento de adelanto- retraso (lead-lag) y contiene un retraso de primer orden y un adelanto de primer orden.

Los sistemas de procesos fluidos y térmicos, manifiestan varias características dinámicas distintas, pero muchas de ellas se pueden describir por combinaciones de cinco funciones de transferencia

K Elemento proporcional

e^-Ls Elemento de tiempo muerto (retardo en el tiempo)

6.2 MODELAMIENTO MATEMÁTICO DE SISTEMAS DINÁMICOS

Para estudiar los sistemas de control una etapa principal es modelar y analizar las características dinámicas del proceso a ser controlado. Un modelo matemático de un sistema dinámico se define como un juego de ecuaciones que representan la dinámica del sistema con exactitud, o al menos, razonablemente bien. Un sistema dado puede tener muchos modelos matemáticos.

La dinámica de muchos sistemas se pueden describir en términos de ecuaciones diferenciales, y la respuesta del sistema a una entrada se puede obtener si se resuelven las ecuaciones diferenciales que modelan dicho sistema.

Para obtener información detallada sobre modelamiento y simulación de procesos químicos se recomienda revisar el texto del autos sobre: Modelamiento y Simulación de Procesos

Ejemplo 6.1

Modelamiento matemático de un intercambiador de calor.

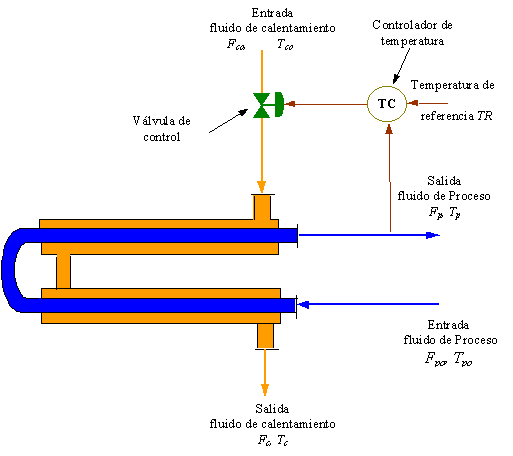
Fig. 6.1 Sistema de control de Un Intercambiador de Calor

Para ilustrar el modelamiento del proceso, consideraremos el caso de control de temperatura en un intercambiador de calor de doble tubo. En un sistema de intercambio de calor, generalmente se tiene como objetivo calentar (o enfriar) un fluido de proceso hasta una temperatura determinada T_p (de salida) para ser alimentado a una etapa posterior en el proceso, para cumplir con este objetivo se debe usar una corriente de fluido de calentamiento (o enfriamiento) el cual debe operar en un rango de temperaturas entre la entrada T_co y la salida T_c y a una velocidad de flujo F_c, la cual depende de los requerimientos del proceso.

Si el objetivo del proceso de transferencia de calor es el calentamiento (o enfriamiento) de la corriente de proceso, el objetivo del sistema de control es mantener la temperatura de salida de la corriente de proceso en un valor especificado o en estado estacionario ante cualquier perturbación que pueda alterar el proceso.

Con lo expuesto anteriormente podemos establecer que la variable controlada es la temperatura de salida del fluido de proceso (T_p), y la variable manipulada es la velocidad de flujo del fluido de calentamiento (F_c). Las perturbaciones pueden presentarse debido a cambios en la temperatura de entrada (T_po), la velocidad de flujo (F_p) del fluido de proceso, variación de temperatura del medio ambiente, resistencias a las incrustaciones, etc.

Para el sistema de control del intercambiador de calor dado en la Fig. 6.1, por modelamiento matemático (ver Modelamiento y Simulación de Procesos del mismo autor), se llega a las Ecs. (6.16) y (6.17)

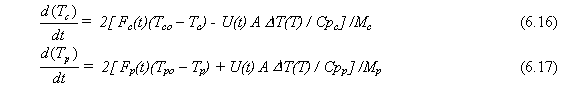
donde T_c = temperatura de salida del fluido caliente

T_c0 = temperatura de entrada del fluido caliente

T_p = temperatura de salida del fluido de proceso (variable que se va a controlar)

T_p0 = temperatura de entrada del fluido de proceso

F_c = flujo de masa del fluido caliente (variable que se va a manipular)

F_p = flujo de masa del fluido de proceso

U = coeficiente total de transferencia de calor

A = área de transferencia de calor

DT = diferencia verdadera de temperaturas

Cp_c = capacidad calorífica del fluido caliente

Cp_p = capacidad calorífica del fluido de proceso

M_c = masa del fluido caliente dentro del intercambiador

M_p = masa del fluido de proceso dentro del intercambiador

t = tiempo

T = (T_c, T_Co, T_p, T_po) es un vector de temperaturas de los fluidos de entrada y salida, DT(T) es la diferencia media efectiva de temperaturas, la cual puede ser la diferencia media aritmética de temperaturas (DMAT).

DT(T) = [(T_p – T_co) + (T_po –T_c)]/2 (6.18)

o como en la mayoría de los casos prácticos, la diferencia media logarítmica de temperaturas (DMLT).

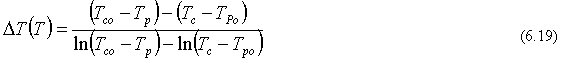
La dependencia del tiempo del coeficiente de transferencia de calor es importante para variaciones en el área de transferencia de calor. En este caso asumimos que U(t) ¹ 0, t ³ 0 y T_co> T_po ó (T_co< T_po respectivamente). Las asunciones precedentes implican que bajo condiciones normales de operación, T_co> T_c o (T_co< T_c respectivamente), de modo que el sistema de control está bien definido para todo t > 0.

Ejemplo 6.2

Modelamiento matemático de tres reactores en serie

Fig. 6.2 Reactores CSTR en serie

La Fig. 6.2 muestra una batería de tres reactores en serie. El producto B es formado y el reactante A es consumido en cada uno de los tres reactores perfectamente mezclados mediante una reacción de primer orden llevándose a cabo en el liquido. Por el momento asumimos que las temperaturas y retenciones (volúmenes) de los tres tanques pueden ser diferentes, pero tanto las temperaturas y el volumen de liquido en cada tanque se asumen a ser constantes (isotérmico y a volumen constante). Se asume densidad constante a lo largo del sistema, el cual es una mezcla binaria de A y B.

Con estas asunciones en mente, podemos formular nuestro modelo. Ver Modelamiento y Simulación de Procesos del mismo autor.

Las ecuaciones que describen los cambios dinámicos en las cantidades de reactante A en cada tanque son (con unidades de Kg. . mol de A/min)

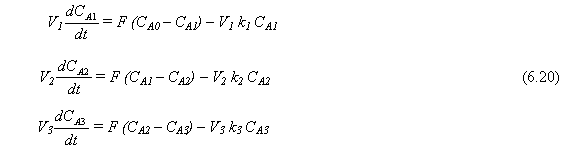
La velocidad de reacción específica k_n está dada por la ecuación de Arrhenius

k_n = a n = 1, 2, 3 (6.21)

si las temperaturas en los reactores son diferentes, los k son diferentes. La n se refiere al número de la etapa.

El volumen V_n puede ser sacado fuere de la derivada del tiempo debido a que es constante. Si el flujo F es constante y las retenciones y temperaturas son las mismas en todos los tanques, las Ec. (6.20) serán

(6.22)

donde t = V/F con unidades de minutos

Existe solamente una función impulsora o variable de entrada C_A0_.

6.3 SISTEMAS LINEALES Y NO LINEALES

6.3.1 Sistemas lineales

Un sistema en el que se aplica el principio de superposición se denomina lineal. El principio de superposición establece que la respuesta producida por la aplicación simultánea de dos funciones excitadoras (perturbaciones) distintas, es la suma de las respuestas individuales. Por lo tanto, para sistemas lineales la respuesta a diversas entradas se puede calcular tratando una entrada a la vez, y añadiendo o sumando los resultados.

La primera interrogante que debe ser contestada es justamente cuando una ecuación diferencial es lineal. Básicamente es la que contiene variables solamente elevadas a la primera potencia en cualquiera de los términos de la ecuación.

Ejemplo de EDO lineal

(6.23)

donde a_o y a₁ son constantes o funciones del tiempo solamente, no de las variables dependientes o sus derivadas.

6.3.2 Sistemas no lineales

Los procesos reales generalmente se modelan mediante ecuaciones algebraicas y/o diferenciales no lineales. Si en la ecuación aparecen raíces cuadradas, cuadrados, exponenciales, productos de variables, etc., la ecuación, es no lineal.

Ejemplos de EDO no lineal

(6.24)

(6.25)

(6.26)

(6.27)

donde x₁ y x₂ son variables dependientes

6.4 LINEALIZACIÓN

Matemáticamente, una ecuación diferencial lineal es una para la cual se cumplen las siguientes propiedades:

Si x(t) es una solución, entonces cx(t) es también una solución, donde c es una constante.
Si x₁ es una solución y x₂ es también una solución, entonces x₁ + x₂ es una solución.

La linealización es muy simple. Todo lo que se tiene que hacer es tomar las funciones no lineales, expandirlas en una serie de expansión de Taylor alrededor de la operación al estado estacionario, y despreciar todos los términos después de las primeras derivadas parciales.

Asumiendo que tenemos una función no lineal de variables del procesos x₁ y x₂: f ₍_x_1,_x₂₎. Por ejemplo, x₁ podría ser fracción molar o temperatura o razón de flujo. Denotando los valores de estas variables al estado estacionario como:

x_1s = valor al estado estacionario de x₁

x_2s = valor al estado estacionario de x₂

Ahora expandiendo la función f₍_x_1,_x₂₎ alrededor de sus valores al estado estacionario f ₍_x_1s,_x_2s).

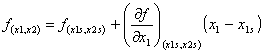
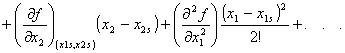(6.28)

La linealización consiste en truncar las series después de las primeras derivadas parciales.

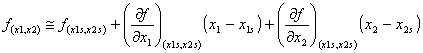(6.29)

Hemos aproximado la función real a una función lineal

Ejemplo 6.3

Considerar la dependencia del flujo saliendo de un tanque a la raíz cuadrara de la altura de liquido en el tanque:

(6.30)

La serie de expansión de Taylor alrededor del valor de h al estado estacionario, el cual es h_s en nuestra nomenclatura es:

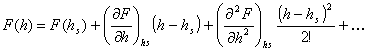(6.31)

(6.32)

(6.33)

Ejemplo 6.4

El producto de dos variables dependientes es una función no lineal de dos variables:

f(C_A, F) = C_A F (6.34)

Linealizando

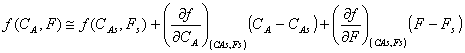(6.35)

C_A(t)F(t) @ C_As F_s +F_s(C_A(t) – C_As) + C_As(F(t) – F(s)) (6.36)

Notar que la linealización convierte la función no lineal (el producto de dos variables dependientes) en una función lineal conteniendo dos términos.

6.5 VARIABLES DE DESVIACIÓN

Nosotros encontraremos de mucha utilidad en prácticamente todos los casos de estudio de dinámica y control de sistemas lineales tomar la variable de desviación del estado estacionario en lugar de las variables absolutas

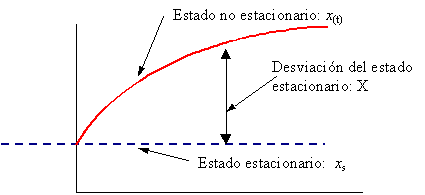
Fig. 6.3 Variables de desviación

Como las variables totales son funciones del tiempo, x_(t), su desviación de los valores del estado estacionario x_s también serán funciones del tiempo como muestra la Fig. 6.3.

Esta desviación del estado estacionario se denomina desviación o variables de desviación. Nosotros usaremos letras mayúsculas para denotar las variables de desviación. Entonces, la variable de desviación X es definida como:

X = x(t) – x _s (6.37)

Las ecuaciones que describen al sistema lineal pueden ser ahora expresadas en términos de estas variables de desviación. Cuando se hace esto, dos resultados muy útiles ocurren

Los términos en la ecuación diferencial ordinaria tienen las constantes fuera
las condiciones iniciales para las variables de desviación son todas iguales a cero si el punto de inicio es la condición de operación al estado estacionario.

6.6 FUNCIÓN DE TRANSFERENCIA DE LOS ELEMENTOS DE UN SISTEMA DE CONTROL

Para el análisis de sistemas de control, se considera la carga constante y se varia el setpoint, y el sistema de control debe llevar el valor de la variable de salida al valor dado del setpoint. Con esta consideración, el sistema de control del intercambiador de calor dado en el Ejemplo 6.1. puede representar mediante un diagrama de bloques para una operación servo (discutida en el punto 6.13)

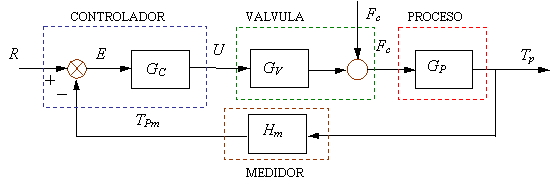
Fig.6.4 Diagrama de bloques del sistema de control

Como se puede observar en la Fig. 6.4, el sistema de control es un sistema de lazo cerrado con retroalimentación en el cual se mide la variable controlada (salida) para compararlo con el valor deseado de esta variable (valor de referencia), esto se hace en el comparador y debido a que en la comparación la variable medida entra con signo negativo, este sistema se conoce como “feedback negativo”.

Para un sistema de retroalimentación (feedback) negativo, la señal medida proveniente del sensor ingresa con signo negativo al comparador por lo que el error está dado por:

Error = valor de referencia o al E.E. (setpoint) – señal medida (6.38)

En este texto usaremos la siguiente nomenclatura:

a) En el dominio del tiempo

r(t) = setpoint

y_m(t) = variable medida

e(t) = error

e(t) = r(t) – y_m(t) (6.39)

b) En el dominio de Laplace y usando las variables de desviación:

R(s) = setpoint

Y_m(s) = variable medida

E(s) = error

E(s) = R(s) – Y_m(s) (6.40)

Si hay diferencia se produce una señal de error la cual va al controlador para accionar la válvula de control y regular el flujo del fluido de calentamiento según lo requerido por el proceso.

Como muestra este sistema de control, los elementos básicos son:

– Proceso

– Elemeto de medida (Sensor)

– Controlador

– Elemento final de control (Válvula)

– Elementos de transporte de señal

Siendo estos los elementos del sistema, veremos en el presente capítulo como deducir las funciones de transferencia de cada elemento.

6.6.1 Función de transferencia del proceso

La función de transferencia para el proceso controlado relaciona en el dominio de Laplace a la variable controlada (salida) a la variable manipulada (entrada).

Ejemplo 6.5

Función de transferencia de un intercambiador de calor

La función de transferencia para el proceso controlado llevado a cabo en el intercambiador de calor debe relacionar en el dominio de Lapace a la variable de salida (controlada) T_p a la variable de entrada (manipulada) F_c. De la Ec. (6.16) (para el fluido de proceso), considerando constante el flujo de entrada

= (T_po – T_p) + U(t) A DT(T) /F_p Cp_p (6.41)

si = t_p (tiempo) y A DT(T) /F_p Cp_p = k₁

La Ec. (6.25) se puede escribir como

+ T_p = T_po + k₁ U (6.42)

En el estado estacionario, la Ec. (6.41) será:

+ T_ps = T_pos + k₁ U_s = 0 (6.43)

Donde el subíndice s indica al estado estacionario. Restando la Ec. (6.43) de la Ec. (6.42) se tiene

+ (T_p – T_ps ) = (T_po – T_pos ) + k₁ (U – U_s ) (6.44)

Definiendo las variables de desviación para el intercambiador de calor:

(T_p – T_ps ) = T_p

(U – U_s ) = U

Además, T_po = T_pos la temperatura de entrada es la misma en cualquier instante. Con lo cual la Ec. (6.44)será:

+ T_p = k₁ U (6.45)

Aplicando la transformada de Laplace a la Ec. (6.45) se tiene:

t_p [ s T_p (s) – T_p (0) ] + T_p (s) = k₁ U(s) (6.46)

Donde T_p (0) = 0, ya que en el tiempo cero recién se inicia el proceso y no hay variación del estado estacionario (las variables de desviación para t = 0 son 0). Simplificando la Ec. (6.46) se tiene

(6.47)

donde: t_p= Constante de tiempo del proceso (usualmente minutos o segundos)

k₁ = Ganancia al estado estacionario

Usando el mismo procedimiento para la Ec. (6.17) (fluido de calentamiento) y aplicando la propiedad de traslación de la transformada, para lo cual se sabe que:

Q = F_c (T_c – T_co) = U A DT (6.48)

se tiene la función de transferencia para el fluido de calentamiento

(6.49)

Considerando que los dos procesos se llevan a cabo en serie, por lo cual la función de transferencia del proceso total será el producto de las funciones de transferencia individuales, y haciendo k₁ k₂ = K_p, t_c = t₁ y t_p = t₂, se tiene:

; t₁ , t₂ > 0 (6.50)

La Ec. (6.50), relaciona la variable de salida T_P (variable controlada) a la variable regulada F_C (entrada o carga), donde t₁ y t₂ son las constantes características de tiempo del proceso. Esta función de transferencia es de segundo orden.

Ejemplo 6.6

Función de transferencia de un sistema de nivel de liquido

Al analizar sistemas que consideran el flujo de fluidos, se hace necesario dividir el régimen de flujo en régimen de flujo laminar y régimen de flujo turbulento, de acuerdo con la magnitud del número de Reynolds. Si el número de Reynolds es mayor que aproximadamente 3000 – 4000, el flujo es turbulento.

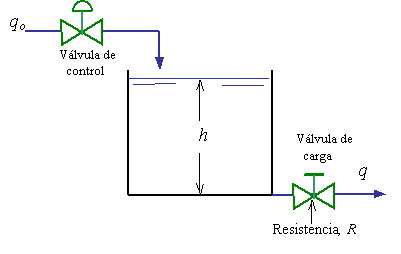
Fig. 6.5 Sistema de control de nivel de liquido

donde: q = caudal de entrada, en m³ / s

q_o = caudal de salida, en m³ / s.

h = nivel de liquido, en m.

R = resistencia a la salida

A = área de sección transversal del tanque, m²

V = volumen de liquido en el tanque, m³

Si el Reynolds es menor que aproximadamente 2000, el flujo es laminar. En el caso laminar el flujo de fluido se produce en tuberías sin turbulencia. Los sistemas que implican flujo turbulento suelen requerir, para representarse, de ecuaciones diferenciales no lineales, mientras que los sistemas que corresponden a flujo laminar, pueden representarse por ecuaciones diferenciales ordinarias. (En los procesos industriales frecuentemente se tiene flujos en tuberías y tanques. En esos procesos el flujo es frecuentemente turbulento y no laminar).

a) Caso lineal

Como se ha mencionado anteriormente, un sistema se puede considerar lineal si el flujo es laminar. En este caso la resistencia al caudal de salida es lineal y estará dado por:

q_o = R h (6.51)

El sistema debe mantener constante el nivel de liquido en el tanque (salida) para lo cual debe regular el caudal de entrada (entrada). Por lo tanto la función de transferencia debe relacionar en el dominio de Laplace el nivel de liquido al caudal de entrada.

Función de transferencia:

(6.52)

1. Haciendo un balance de materiales al estado no estacionario

entrada – salida = acumulación (6.53)

(6.54)

V = Ah; dV = Adh y q_o = h/R

q – q_o = q – h/R = A

(6.55)

definiendo la constante de tiempo, AR = t, la Ec. (6.55) se escribe:

(6.56)

2. Haciendo un balance de materiales al estado estacionario

(6.57)

donde h_s = nivel de liquido en el estado estacionario

q_s = caudal de entrada en el estado estacionario

1. Definiendo las variables de desviación, para lo cual restamos la Ec. (6.57) de la Ec. (6.56) se tiene:

(6.58)

Las variables de desviación están dadas por:

(h – h_s) = H

(q – q_s) = Q

con lo cual la Ec. (6.58) se escribe:

(6.59)

2. Tomando la transformada de Laplace a la Ec. (6.59) se tiene:

t[sH(s) – H(0)] + H(s) = RQ(s)

Como se ha visto anteriormente, H(0) = 0 con lo cual se tiene:

t sH(s) + H(s) = RQ(s)

H(s) [ts + 1] = R Q(s)

(6.60)

Función de transferencia que relaciona el nivel de liquido al caudal de entrada

b) Caso no lineal

Supongamos que el tanque del ejemplo anterior opera en régimen turbulento por lo que posee una resistencia no lineal en la salida, y el caudal de salida está dado por:

q₀ = R h^1/2 (6.61)

De igual manera que en el caso anterior, la función de transferencia del proceso debe relacionar en el dominio de Laplace el nivel de liquido al caudal de entrada.

Función de transferencia:

(6.62)

Haciendo un balance de materiales al estado no estacionario igual que en el caso lineal

(6.63)

V = Ah; dV = Adh y q_o = C h^1/2

q – q_o = q – Ch^1/2= A (6.64)

Como existe él termino NO LINEAL Ch^1/2 trae dificultades al momento de tomar la transformada de Laplace, por lo que esta ecuación debe linealizarse.

Para esto hacemos uso de la serie de expansión de TAYLOR y la función q₀(h) puede ser expresada en las proximidades del estado estacionario para valores de h próximos a h_s.

Entonces

q_o = q_o(h_s) + q¢_o(h_s)(h – h_s) + . . . (6.65)

donde q’₀(hs) = es la primera derivada de q₀ evaluada a h_s.

q’’₀(hs) = es la segunda derivada de q₀ evaluada a hs constante.

Si tomamos solamente los términos lineales, el resultado es:

q_o @ q_o(h_s) +q¢_o(h_s)(h – h_s) (6.66)

Si sabemos que

q_o = C h^1/2

q¢_o(h_s) = dq_o(h_s)

Reemplazando el valor de q’₀ (h_s) en la Ec. (6.66) tenemos:

(6.67)

Haciendo q_o(h_s) =

Tenemos

(6.68)

Sustituyendo la Ec. (6.68) en (6.65)

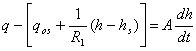
(6.69)

1. Haciendo un balance de materiales al estado estacionario.

(6.70)

2. Restando las Ecs. (6.69) – (6.70)

(6.71)

Introduciendo las variables de desviación

q – q_s = Q

h – h_s = H

(6.72)

Definiendo la constante de tiempo t = AR₁ se tiene:

R₁Q – H = (6.73)

Tomando la transformada de Laplace

R₁Q(s) – H(s) = t[sH(s) – H(0)]

R₁Q(s) – H(s) = t sH(s)

R₁Q(s) = t sH(s) + H(s)

R₁Q(s) = H(s) [ts + 1]

(6.74)

Ejemplo 6.7

Función de transferencia de sistemas térmicos

Sea el sistema que aparece en la Fig. 6.6. Se supone que el tanque está aislado para evitar pérdida de calor al aire circundante. También se supone que no hay almacenamiento de calor en el aislamiento y que el liquido del tanque está perfectamente mezclado, de modo que la temperatura es uniforme. Así que se utiliza un termómetro único para describir la temperatura del liquido en el tanque, y la del liquido que fluye a la salida

Hay tres medios diferentes en que el calor fluye de una sustancia a otra: Conducción, Convección y Radiación.

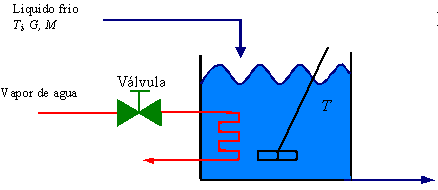
Fig. 6.6 Sistema Térmico

Se define

T_i = temperatura en estado estacionario del liquido que entra, en ^oC

T = temperatura en estado estacionario del liquido que sale, en ^oC

G = gasto de liquido en estado estacionario, en Kg./s.

M = masa de liquido en el tanque, en Kg.

C_p = calor especifico del líquido, en Kcal/Kg.^oC

R = resistencia térmica, en ^oC s/ Kcal

C = capacidad térmica en Kcal/ ^oC

q = flujo de calor, en Kcal/s.

Para este caso, se obtiene qo, C y R respectivamente como:

qo = GC_P T (6.75)

C = MC_p (6.76)

Si se desea instalar un sistema de control para controlar la temperatura de salida (variable controlada), manipulando el flujo de calor (variable manipulada). La función de transferencia que relacione para el proceso debe ser: G(s) = T(s)/Q(s).

Haciendo un balance de energía en el tanque al estado no estacionario

Entrada – Salida = Acumulación

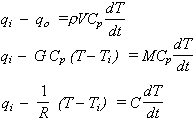
Definiendo la constante de tiempo como: t = RC = M/G, segundos

Escribiendo la Ec. (6.78) al estado estacionario:

Restando la Ec.(6.79) de la Ec. (6.78)

Definiendo las variables de desviación:

(q_i – q_is) = Q

(T – T_s) = T

y con T_i – T_is = 0 La temperatura de entrada se mantiene constante en todo el tiempo

Tomando la transformada de Laplace:

RQ(s) – T(s) = t [sT(s) – T(0)] T(0) = 0

RQ(s) – T(s) = t sT(s)

RQ(s) = t sT(s) + T(s)

RQ(s) = T(s) [t s + 1]

En la práctica, la temperatura del líquido que entra, puede fluctuar y actuar como perturbación de carga. (Si se desea una temperatura constante del flujo de salida se puede instalar un control automático para ajustar el flujo de calor de entrada con el objeto de compensar las fluctuaciones en la temperatura del liquido que ingresa). Si la temperatura del liquido de entrada se varia bruscamente desde T_i a T_i + T, mientras el flujo del calor de entrada q y el gasto de liquido G se mantienen constantes, entonces el flujo de calor de salida se modificará de q a q + q₀ y la temperatura del gasto de salida cambiara de T a T + T_o. El modelo matemático para el proceso, se puede obtener de la misma forma que en el caso anterior, pero en este caso se mantiene constante q_i, pero varía T_i, con lo cual se tiene:

La función de transferencia que liga a T con T_iesta dada por:

Si el sistema térmico está sujeto a variaciones, tanto en la temperatura del líquido que entra como en el flujo de calor de entrada, mientras se mantiene constante el gasto de líquido, el cambio de temperatura T del líquido que sale, se puede obtener de la siguiente ecuación

En la Fig. 6.12, se muestra un diagrama de bloques correspondientes a este caso, (Nótese que el sistema comprende dos entradas).

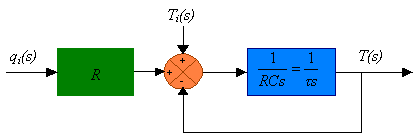
Fig. 6.7 Diagrama de Bloques del Sistema

Ejemplo 6.5

Sistema de mezclado.

Considerar un proceso de mezclado en el cual una corriente de solución conteniendo sal disuelta fluye a un flujo volumétrico constante. La concentración de sal en la corriente de entrada X (masa de volumen) varia con el tiempo.

Si desea obtener la función de transferencia que relacione la concentración de salida con la concentración de entrada.

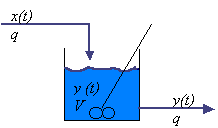
Fig. 6.8 Sistema de mezclado

G(s) = Y(s)/X(s) (6.85)

Asumiendo que la densidad de la solución permanece constante. La concentración de salida debe ser igual a la concentración de la solución dentro del tanque, puesto que es mezclada.

Analizando el sistema y haciendo un balance de sal:

Sal que entra – Sal que sale = Sal acumulada en el tanque

Haciendo un balance de materiales al estado no estacionario tenemos:

donde V = constante

x, y = masa de sal / volumen

q = flujo volumétrico

Haciendo un balance de materiales al estado estacionario tenemos:

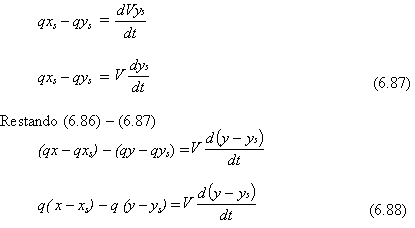
Introduciendo las variables de desviación

x – x_s = X

y – y_s = Y

La Ec. (6.88) se escribe

Aplicando la transformada de Laplace:

X(s) – Y(s) = t [sY(s) – Y(0)]

X(s) – Y(s) = t sY(s)

X(s) = t sY(s) + Y(s)

X(s) = Y(s)[t s + 1

Ejemplo 6.6

Sistema de reacción.

Considerar un reactor CSTR (Reactor Continuo de Tanque Agitado) donde tiene lugar la reacción siguiente:

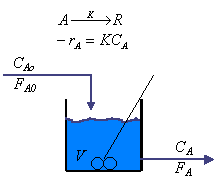
Fig 6.9 CSTR

donde r_a = velocidad de reacción

K = constante de reacción

C_A = concentración de A

V = volumen del reactor

F = caudal volumétrico de alimentación(constante)

C_A0= Concentración inicial de A

N_A = Moles de salida

N_Ao= Moles de entrada

Considerando que la densidad y volumen son constantes, desarrollar la función de transferencia que relacione la concentración en el reactor con la concentración en la alimentación.

Haciendo un balance de materiales a condiciones no estacionarios (base reactante límite A)

Entrada = Salida + Desaparición por reacción + Acumulación

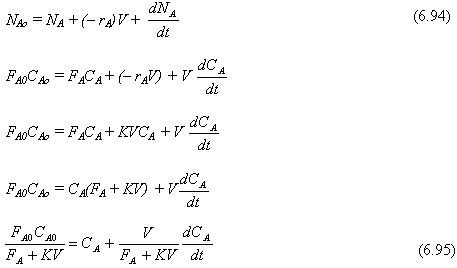
Definiendo como

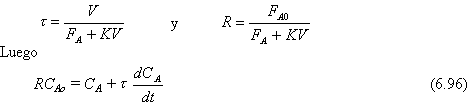
Haciendo un balance de materiales al estado estacionario.

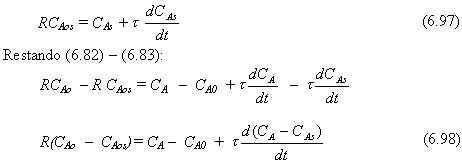
Introduciendo las variables de desviación

C_Ao – C_Aos = C_A0

C_A – C_As = C_A

Luego

Tomando la transformada de Laplace

RC_A0(s) = C_A(s) + t [sC_A(s) + C_A(0)] (6.100)

RC_A0(s) = C_A(s) (1 + t s)

Ejemplo 6.10

Tres reactores CSTR en serie

El sistema es mostrado en la Fig. 6.10 y es una simple extensión del CSTR considerado en el Ejemplo 6.9. El producto B es formado y el reactante A es consumido en cada uno de los tres reactores perfectamente mezclados mediante una reacción de primer orden llevándose a cabo en el liquido. Se asume que las temperaturas y el volumen de liquido en cada tanque son constantes (isotérmico y a volumen constante). Se asume densidad constante en el sistema, el cual es una mezcla binaria de A y B.

Con estas asunciones en mente, podemos formular nuestro modelo. Si el volumen y densidad de cada tanque son constantes, la masa total en cada tanque es constante. Luego la ecuación de continuidad total para el primer reactor es

o F₀ = F₁

Asimismo, un balance total de masa en los tanques 2 y 3 da

F₃ = F₂ = F₁ = F₀ = F (6.103)

Donde F se define como el flujo (m³/min)

Fig. 6-10 Reactores CSTR en serie

Si se quiere determinar las cantidades de reactante A y producto B en cada tanque, son necesarias las ecuaciones de continuidad por componente. Sin embargo, como el sistema es binario y se conoce la cantidad total de masa de material en cada tanque, solamente es necesaria una ecuación de continuidad de componente. Se pueden usar ya sea A o B. Si elegimos arbitrariamente A, las ecuaciones que describen los cambios dinámicos en las cantidades de reactante A en cada tanque son (con unidades de kg . mol de A/min)

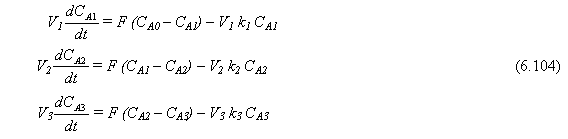
La velocidad de reacción específica k_n está dada por la ecuación de Arrhenius

si las temperaturas en los reactores son diferentes, los k son diferentes. La n se refiere al número de la etapa.

Las tres ecuaciones diferenciales de primer orden no lineales dadas en la Ecs. (6.104) son el modelo matemático del sistema.

Usaremos este sistema simple en muchas partes subsecuentes de este libro. Si se usa para diseño de sistemas de control y para análisis de estabilidad, se usará una versión simplificada. Si el flujo F es constante y las retenciones y temperaturas son las mismas en todos los tanques, las Ecs (6.104) serán

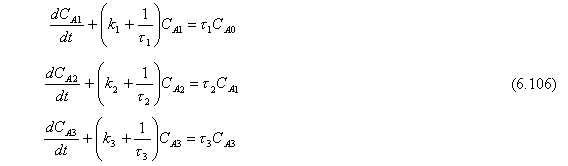
donde t = V/F con unidades de minutos

k = minutos ^–1 (reacción de primer orden)

Existe solamente una función impulsora o variable de entrada C_A0_,y la variable de salida del sistema es C_A.

El sistema considerado anteriormente; Fig. 6.10, es un sistema de “lazo abierto”, es decir, no se usa ningun controlador de retroalimentación.

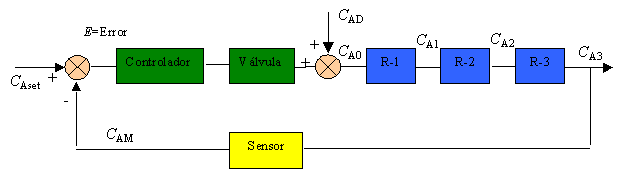
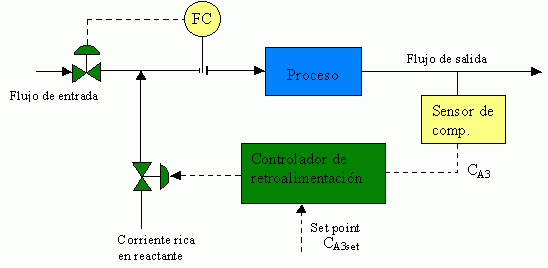
Fig. 6.11 Lazo cerrado para un proceso de tres CSTR. (a) Sistema idealizado; (b) Sistema actual

Si adicionamos un controlador de retroalimentación, tenemos un sistema de “lazo cerrado”; Fig. 6.11.

El controlador mide la concentración saliendo del tercer tanque C_A3 y hace ajustes en la concentración de entrada al primer reactor C_Ao en orden a mantener C_A3 cerca al valor de referencia deseado (“set point”) C_A3set. La variable C_AD es una desviación de la concentración y la variable C_AM es una concentración manipulada que es cambiada por el controlador. Nosotros asumimos que:

C_Ao = C_AM + C_AD (6.107)

Esta es una idealización del sistema físico real en el cual la señal de control desde el controlador deberá mover la posición de la válvula de control que deberá regular una corriente con alta concentración de reactante A hacia la corriente de alimentación (Ver Fig. 6.11)

Reacomodando las Ecs. (6.94) tenemos:

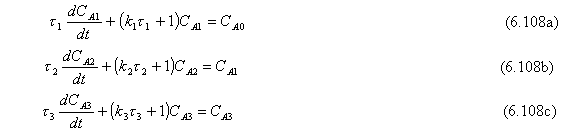
Las variables pueden ser ya sea totales o variables de desviación ya que las ecuaciones son lineales ( todas las k y t con constantes). Nosotros usaremos variables de desviación, y por lo tanto las condiciones iniciales para todas las variables son cero.

C_A1(0)= C_A2(0) = C_A3(0) = 0 (6.109)

Tomando la transformada de Laplace y encontrando la función de transferencia para cada tanque.

Tanque 1:

t₁sC_A1(s) + k₁t₁C_A1(s) + C_A1(s) = C_A0(s)

Tanque 2:

t₂sC_A2(s) + k₂t₂C_A2(s) + C_A2(s) = C_A1(s)

Tanque 3:

t₃sC_A3(s)+ k₃t₃C_A3(s) +C_A3(s) = C_A2(s)

Si nosotros estamos interesados en el sistema total y queremos solamente el efecto de la entrada C_A0 sobre la salida C_A3, las tres funciones de transferencia pueden ser combinadas para eliminar C_A1 y C_A2.

C_A3(s)= G₃ C_A2(s)= G₃(G₂ C_A1(s)) = G₃ G₂ (G₁ C_A0(s) ) (6.111)

La función de transferencia total G(s) es:

Multiplicando las tres funciones de transferencia y reacomodando se tiene:

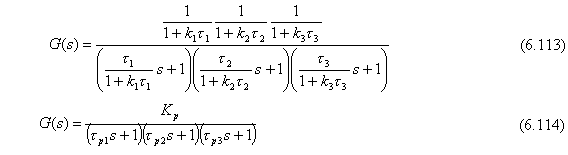
La Ec. (6.114) es la Función de transferencia del proceso total en la forma estándar con las constantes de tiempo t_pi y una ganancia al estado estacionario K_p

Ejemplo 6.11

Dos tanques calentados

El flujo F de aceite pasando a través de dos tanques en serie perfectamente mezclados es constante e igual a 90 pies³/min. La densidad r del aceite es constante e igual a 40 lb_m/ pie³, y su capacidad calorífica C_P es 0,6 Btu/lb_m°F. El volumen del primer tanque V₁ es constante e igual a 450 pies³, y el volumen del segundo tanque V₂ es constante e igual a 90 pies³. La temperatura del aceite entrando al primer tanque es T₀ y es 150 °F en el estado estacionario inicial. Las temperaturas en los dos tanques son T₁ y T₂. Las dos son iguales a 250 °F en el estado estacionario inicial. Un dispositivo de calentamiento en el primer tanque usa vapor para calentar el aceite. Denominando Q₁ al calor adicionado en el primer tanque.

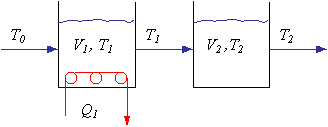
Fig. 6.12 Dos tanques con calentamiento

Se puede hacer un balance de energía para cada tanque,.

Balance de energía para el tanque 1:

Balance de energía para el tanque 2:

Como el flujo a través de los tanques es constante F₀ = F₁ = F₂ = F. Debido a que los volúmenes, densidades, y capacidades caloríficas son todas constantes, las Ecs. (6.115) y (6.116) se pueden simplificar

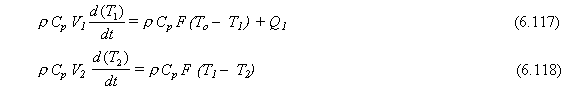
Los valores numéricos de las variables son:

F = 90 pies3/min r = 40 lbm/pie3 C_p = 0.6 Btu/lbm ^oF

V₁ = 450 pies3 V₂ = 90 pies3

Reemplazando estos valores en las Ecs. (6.117) y (6.118) da:

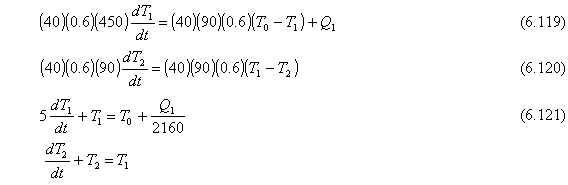
Las transformaciones de Laplace da

(s + 1) T₂ (s) = T₁(s)

Rearreglando y combinando para eliminar T₁ da la variable de salida T₂ como una función de las dos variables de entrada, T₀ y Q₁.

Los dos términos entre corchetes representan las funciones de transferencia de este proceso de lazo abierto. En los siguientes capítulos veremos este sistema nuevamente y usaremos un controlador de temperatura para controlar T₂ manipulando Q₁. La función de transferencia relacionando la variable controlada T₂ a la variable manipulada Q₁ es definida como G_M(s). La función de transferencia relacionando la variable controlada T₂ a la perturbación de carga T₀ es definida como G_L(s).

T₂(s) = G_L(s) T₀(s) + G_M(s) Q₁(s) (6.124)

Estas dos funciones de transferencia son retrazos de segundo orden con constantes de tiempo de 1 minuto y 5 minutos.

6.6.2 Función de transferencia del elemento de medida (sensor)

Los elementos de medida o sensores pueden considerarse como la primera etapa en un sistema de control, y son los que van a reportar el valor de la variable para compararlo con el valor deseado o punto de consigna y determinar el error.

Siendo así la entrada en un elemento de medida es la variable leída (Y) y la salida es el valor emitido hacia el controlador (Y_m), con lo cual la función de transferencia es

Como las características dinámicas y estáticas del sensor o elemento de medición afectan la indicación del valor efectivo de la variable de salida, el sensor juega un papel importante en la determinación del comportamiento global del sistema de control. El sensor suele determinar la función de transferencia en la retroalimentación. Si las constantes de tiempo del sensor son insignificantes en comparación con las constantes de tiempo de los demás componentes del sistema de control, la función de transferencia del sensor se convierte, simplemente en una constante. A continuación se dan ecuaciones de funciones de transferencia más comunes de sensores

La respuesta de un sensor térmico suele ser del tipo sobre amortiguado de segundo orden

Ejemplo 6.12

Función de transferencia de un termómetro de mercurio

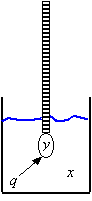
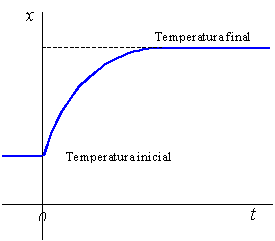
Un ejemplo para ilustrar la función de transferencia de un sensor es un termómetro de mercurio. Cuando se desea tomar la temperatura usando un termómetro de mercurio, se debe esperar un cierto tiempo hasta que el termómetro alcance la temperatura del medio que lo rodea, entes de comenzar a medir la temperatura (colocar el termómetro en el medio que se va a medir) este se encuentra en un estado estacionario, durante el tiempo que demora el termómetro para alcanzar la temperatura del medio, este se encuentra a condiciones no estacionarias y cuando alcanza la temperatura del medio hacia delante se encuentra a condiciones estacionarias.

Fig. 6.13 Comportamiento de un termómetro de mercurio

Considerando: x = temperatura del liquido.

y = temperatura del bulbo del termometro.

A = área superficial del bulbo.

U = coeficiente de transferencia de calor.

m = masa de mercurio en el bulbo.

C_p = capacidad calorífica del mercurio.

1. Un balance de energía para el bulbo de mercurio a condiciones no estacionarias esta dado por:

Calor que entra – calor que sale = acumulación (6.129)

definiendo la constante de tiempo del termómetro como

se tiene:

2. Haciendo un balance de energía al estado estacionario

Restando (6.132) – (6.133)

Definiendo las variables de desviación:

y – y_s = Y

x – x_s = X

La Ec. (6.134) se escribe como

Tomando la transformada de Laplace de la EC. (6.135)

X(s) – Y(s) = t [sY(s) – Y(0)]

Pero Y(0) = 0 todavía no se inicia el cambio

X(s) – Y(s) = t sY(s)

Es la función de transferencia para el termómetro de mercurio

6.6.3 Función de transferencia del controlador

1. Control proporcional PC

La ecuación describiendo un controlador proporcional en el dominio del del tiempo es:

u(t) = u_s ± K_c(r (t) – y_m (t)) (6.137)

donde u = señal de salida del controlador

u_s = constante, señal de salida del controlador al E.E. (cuando el r = y_m, P = P_s)

r = setpoint

y_m = señal medida del proceso desde el transmisor

K_c = ganancia proporcional

Fig. 6.14 Controlador proporcional

La Ec. (6.137) esta escrita en términos de variables totales. Si estamos tratando con variables de desviación, simplemente eliminamos el término p_s. La transformada de Laplace da:

U(s) = ± K_c(R (s) – Y_m (s)) = ± K_c E(s) (6.138)

donde E = señal de error = R – Y_m

Reacomodando para conseguir la salida sobre la entrada da la función de transferencia G_C(s) para el controlador.

Así, la función de transferencia para un controlador proporcional es simplemente una ganancia.

Sin importar el mecanismo en sí y la potencia que lo alimenta, el controlador proporcional es esencialmente un amplificador con ganancia ajustable. En la Fig. 6.15; se puede ver un diagrama de bloques de este controlador.

Fig. 6.15 Diagrama de Bloques de un Controlador Proporcional

La ganancia del controlador proporcional es la relación que existe entre la variación de la señal de salida y el error que la produce, es decir, es la variación en la señal de entrada. El controlador proporcional es esencialmente un amplificador con ganancia ajustable.

En lugar de la ganancia, muchos controladores emplean la denominada banda proporcional que es la inversa de la ganancia, según la fórmula:

BP % = (100/K)% (6.140)

y cuya definición es:

Banda proporcional es el porcentaje de variación de la variable controlada necesaria para provocar una carrera completa del elemento final de control. Por ejemplo, en el caso de un instrumento de escala 0 – 200 ^oC, en el que basta una variación de temperatura de 50 ^oC para dar lugar a una carrera completa de la válvula de control, la correspondiente banda proporcional es de

En los instrumentos de control industrial la banda proporcional oscila del 1% al 500%, y solo en casos muy espaciales los valores son mayores.

Ejemplo 6.13

Un controlador proporcional se usa para controlar temperatura dentro del rango de 60 a 100 ^oF. El controlador se ajusta de tal manera que la presión de salida vaya desde 3 psi (válvula completamente abierta) hasta 15 psi(válvula completamente cerrada) a medida que la temperatura medida va desde 71 a 75 ^oF con el “set point”mantenido constante. Encontrar la ganancia y la banda proporcional.

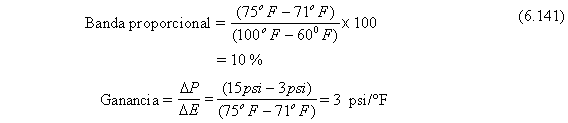
Ahora asumimos que la banda proporcional del controlador es cambiada a 75 por ciento. Encontrar la ganancia y el cambio de temperatura necesario para causar que la válvula vaya de completamente abierta a completamente cerrada.

DT = (banda proporcional)(rango)

= 0,75 (40^oF)

= 30^oF

Control encendido-apagado (on-off). El controlador más simple podría ser un controlador encenido-apagado. En este sistema de control el actuador tiene sólo dos posiciones fijas, que en muchos casos son, simplemente conectando y desconectando.

Un ejemplo de esta acción de control lo constituye una válvula que actúa como un interruptor; si la ganancia proporcional es muy alta la válvula se moverá de una posición extrema a la otra (enteramente cerrada a enteramente abierta).

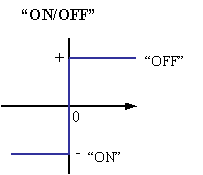
Fig. 6.16 Acción “ON”/ “OFF”

Esta acción muy sensible es llamada acción encendido-apagado “ON/OFF” debido a que la válvula estará enteramente abierta “ON” o enteramente cerrada “OFF”. La válvula en este caso actúa como un interruptor. La anchura de banda de un controlador “ON/OFF” es aproximadamente igual a cero.

El Controlador de dos posiciones es simple y económico razón por la cual se usa en muchos sistemas de control tanto domésticos como industriales.

Sea:

u(t) = señal de salida del controlador.

e(t) = señal de error.

En un controlador de dos posiciones, la señal u(t) permanece en un valor máximo o mínimo, según sea la señal de error positiva o negativa, de manera que:

u(t) = U₁ para e(t) > 0

u(t) = U₂ para e(t) < 0

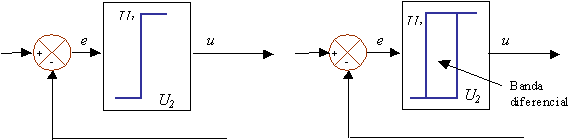
Fig. 6.17 (a) y (b) Diagramas de Bloques de Controladores de Dos Posiciones

Donde U₁ y U₂ son constantes. Generalmente el valor mínimo de U₂ puede ser, o bien cero, o –U₁. En general los controladores de dos posiciones son dispositivos eléctricos, donde habitualmente hay una válvula accionada por un solenoide eléctrico. El rango en que la señal de error debe variar antes que se produzca la conmutación, se denomina zona muerta o brecha diferencial como se indica en la Fig. 6.17(b). Este es un controlador simple y es ejemplificado por el termostato de un sistema de refrigeración. Tal brecha diferencial hace que la salida del controlador u(t) mantenga su valor hasta que la señal de error haya rebasado ligeramente el valor 0.

Offset.. El “offset” es una característica indeseable inherente al control proporcional. Consiste en la estabilización de la variable en un lugar no coincidente con el punto de consigna, después de presentarse una perturbación en el sistema. Inicialmente parece un contrasentido que la variable no se estabilice en el punto de consigna, ya que da la impresión que el controlador no controla, puesto que, aparentemente, lo lógico es que al fijar un punto de consigna la variable vuelva al mismo después de una perturbación.

Veremos con dos ejemplos sencillos el porque se produce el “offset” debido a las características propias del controlador proporcional.

Sea el control de nivel de la Fig. 6.18, realizado mediante una válvula autorreguladora de flotador en la que el flotador está ligado a la válvula mecánicamente. En el supuesto de que el caudal de salida sea igual al caudal de aportación, el nivel se mantendrá en un valor estable que suponemos es igual al punto de consigna. Si en un momento determinado aumenta el caudal de salida por una mayor demanda, el nivel bajará hasta estabilizarse en un nuevo valor, tal que el caudal mayor de entrada por la nueva posición de la válvula de control iguale al caudal de salida. Debido al enlace mecánico entre la válvula y el flotador, el mayor caudal de aportación sólo puede obtenerse con un descenso del nivel que equivaldrá al “offset”.

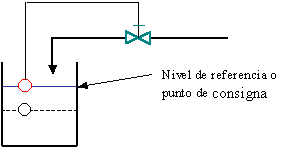
Fig. 6.18 Control de nivel

En el intercambiador de calor de la Fig. 6.19, suponemos que inicialmente la temperatura coincide con el punto de consigna de 100 ⁰C. Al cabo de un tiempo se presenta un cambio de carga, originado, por ejemplo, por un aumento en el consumo de fluido caliente, por apertura simultánea de mayor número de válvulas de consumo.

Nótese que la temperatura no vuelve al valor de consigna, sino que la misma se estabiliza a los 90 ^oC. Es obvio que la temperatura final difiere de la primitiva, puesto que se así no fuera, por las características del control proporcional, la posición de la válvula sería la inicial, lo cual es imposible ya que en esta posición se ha presentado la disminución de temperatura inicial y existiría el absurdo de mantener la misma temperatura de salida con la válvula de control en la misma posición, dando el mismo paso de caudal de vapor tanto para el consumo de agua caliente en el régimen inicial como para el aumento de este consumo.

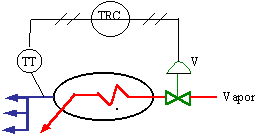
La desviación puede eliminarse reajustando manualmente el punto de consigna; no obstante, si vuelven a cambiar las condiciones de servicio volverá a presentarse el “offset”. De aquí que el control proporcional solo puede aplicarse si las condiciones de servicio no varían y son estables o si la presencia del “offset”en la variable es perfectamente admisible, tal como ocurre, por ejemplo, en el caso del control de nivel de un tanque intermedio en un proceso de fabricación; no importará demasiado que el nivel se estabilice en el 45 % aunque el punto de consigna sea 50 % del nivel del tanque.

2. Control proporcional – integral PIC

La acción de un controlador proporcional – integral queda definida por la siguiente ecuación:

donde t_i = tiempo de restauración, minutos

La Ec. (6.142) está en términos de variables totales. Convirtiendo a variables de desviación y tomando la transformada de Laplace se tiene:

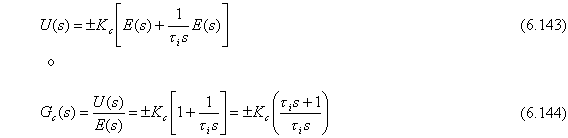
Entonces, la función de transferencia para un controlador PI contiene un adelanto de primer orden y un integrador. Esta es una función de s, conteniendo polinomios de orden uno en el numerador y denominador.

Ambos valores, K_c y t_i son ajustables. El tiempo integral regula la acción de control integral, mientras que una modificación en K_c afecta tanto a la parte integral como a la proporcional de la parte de control.

El recíproco del tiempo integral t_i recibe el nombre de frecuencia de reposición la cual viene hacer la cantidad de veces por minuto que se repite la acción proporcional.

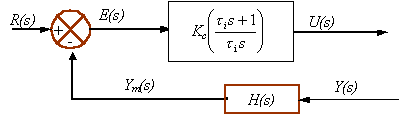
Fig. 6.20. Diagrama de Bloques de un controlador proporcional – integral

En el control integral, el elemento final se mueve de acuerdo con una función integral en el tiempo de la variable controlada, es decir, el movimiento de la válvula corresponde a la suma de las áreas de desviación de la variable con relación al punto de consigna. Por tanto queda eliminado el “offset” típico de la acción proporcional, ya que si se presenta, el controlador integra el área de desviación, moviendo la válvula lo necesario para volver la variable al punto de consigna.

3. Control proporcional – integral – derivativo PIDC

La combinación de los efectos de acción proporcional, integral y derivativa, se denomina acción de control proporcional – integral – derivativa. Esta combinación tiene las ventajas de cada una de las tres acciones de control individuales. La ecuación de un control con esta acción de control es:

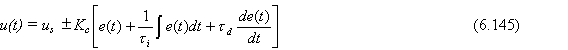
La Ec. (6.145) está en términos de variables totales. Convirtiendo a variables de desviación y tomando la transformada de Laplace se tiene la función de transferencia de un PID “ideal”. La función de transferencia es

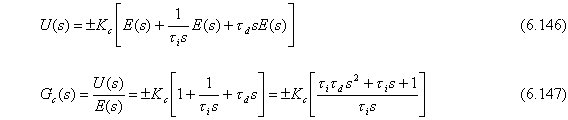
La función de transferencia de un PID “real”, en distinción a uno “ideal”, es la función de transferencia del PI con un elemento de adelanto-retraso colocado en serie.

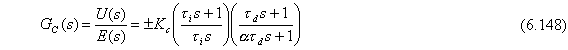
donde t_d = constante de tiempo derivativo, minutos.

a = una constante = 0.1 a 0.05 para la mayoría de controladores comerciales

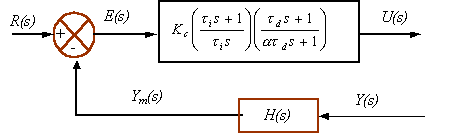
Fig. 6.21 Diagrama de Bloques de un Controlador Proporcional – Integral – Derivativo

La unidad de adelanto-retraso es denominada unidad derivativa, y su respuesta a escalón es mostrada en la Fig. 6.22. para una unidad de escalón de cambio en la entrada, la salida cambia a 1/a y luego decae a una velocidad que depende de t_d. Así la unidad derivativa se aproxima a una derivada ideal. Esto es físicamente realizable ya que el orden del polinomio de su numerador es igual al orden del polinomio de su denominador.

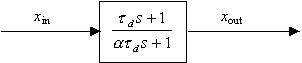
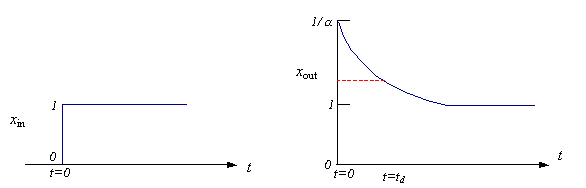
Fig. 6.22 Unidad derivativa

6.6.4 Función de transferencia del elemento final de control (válvula)

El elemento de control final es el mecanismo que altera el valor de la variable regulada, en respuesta a la señal de salida que se obtiene de un dispositivo de control de manejo manual o por alguna manipulación manual directa.

En instalaciones de control automático; éste consta normalmente de dos partes Un activador que traduce la señal de salida del dispositivo controlador en una acción que comprende una gran fuerza o la manipulación de una energía de gran magnitud, y un dispositivo que responde a la fuerza del activador y que ajusta el valor de la variable regulada. Por ejemplo: el activador se puede usar para cambiar la posición de un tapón de válvula en un orificio, la velocidad de un dispositivo giratorio o la cantidad de energía que se suministra a una carga eléctrica.

En el control automático de procesos, el elemento de control final que se emplea con mayor frecuencia es la válvula de diafragma motor (VDM). Consta de un activador neumático de diafragma motor y una válvula de control del fluido de proceso.

Cada dispositivo que se utiliza para constituir un elemento de control final posee sus propias características de retardación dinámica o constantes de tiempo. Esto quiere decir que los dispositivos no responderán de manera instantánea a los cambios de las señales de control o a las perturbaciones de la carga. La importancia del efecto de los retrasos depende del proceso en que se emplea el dispositivo. En algunos casos, estos retrasos pueden degradar gravemente el funcionamiento del sistema de control y por lo tanto, provocar menguas en los buenos resultados del proceso. También pueden hacer que se requiera mayor atención e intervención del operador.

Válvulas de control

En cualquier estudio de válvulas de control y sus características, se deben tomar en cuenta dos partes de la válvula en forma especial: Primero, el cuerpo de la misma, sus aspectos geométricos y los materiales de construcción y en segundo lugar, el macho o tapón de la válvula, su geometría y sus materiales de construcción. La geometría combinada del cuerpo y el tapón determinan las propiedades de flujo de la válvula.

La mayoría de las válvulas operan por medio de un actuador de posición lineal o alguna modificación de este tipo de actuador. Estos actuadores colocan el macho de la válvula en el orificio, en respuesta a una señal proveniente del controlador automático o a través de un ajuste mecánico manual.

Una válvula neumática siempre tiene algún retraso dinámico, el cual hace que el movimiento del vapor no responda instantáneamente a la presión aplicada desde el controlador. Se ha encontrado que la relación entre el flujo y la presión para una válvula lineal puede a menudo representarse por una función de transferencia de primer orden; esto es:

Donde Q(s) = variable manipulada

U(s) = señal proveniente del controlador ( presión o mA) y actúa sobre la válvula

K_V = constante de válvula (ganancia al estado estacionario)

t _V = Constante de tiempo de la válvula

En muchos sistemas prácticos, la constante de tiempo de la válvula es muy pequeña comparada con las constantes de tiempo de otros componentes del sistema de control, y la función de transferencia de la válvula puede ser aproximada a una constante

Bajo estas condiciones, la válvula contribuye con un retardo dinámico despreciable.

Ejemplo 6.14

Para justificar la aproximación de una válvula rápida mediante una función de transferencia la cual se simplifica a K_v, considerar una válvula de primer orden y un proceso de primer orden conectados en serie como muestra la Fig. 6.23

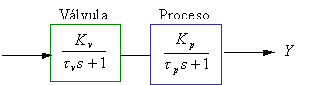
Fig. 6.23 Diagrama de bloques para una válvula de primer orden y un proceso de primer orden

Como se verá mas adelante según el álgebra de bloques, la función de transferencia Y(s)/U(s) es

Para un cambio de una unidad de escalón en U

El inverso de esta ecuación es

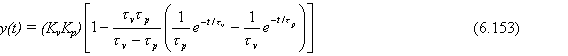
Si t_v << t_p, esta ecuación es aproximadamente

y(t) = (K_vK_p)(1 – e^-t/tp) (6.154)

La última expresión es la respuesta de la función de transferencia

a una unidad de escalón, de tal manera que la combinación de la válvula y el proceso es esencialmente de primer orden. Esto claramente demuestra que, cuando la constante de tiempo de la válvula es muy pequeña comparada a la del proceso, la función de transferencia de la válvula puede ser tomada como K_v.

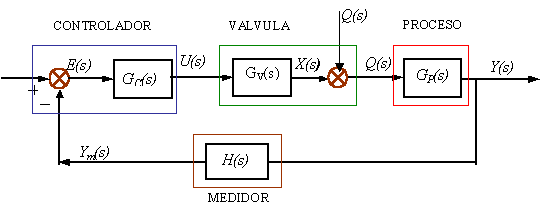
Fig. 6.24 Bloque generalizado: X(s) es la posición del vástago de la válvula y Q(s) el flujo de fluido de proceso producido por la ubicación instantánea del vástago.

Actuadores de posición final

Según la definición antes establecida para el desarrollo de control final, el actuador es un transductor. Este dispositivo se encarga de transducir la señal de control de una forma o un nivel de energía o potencia a otra, por ejemplo: de señal neumática a acción mecánica que se utiliza para regular una variable de proceso. En casi todos los casos, el actuador de válvula se puede clasificar como actuador de posición lineal. Suministra una posición de salida que es proporcional a una señal de entrada. El movimiento del elemento de salida del activador es, casi siempre, de translación (en oposición o rotacional), aunque el movimiento de translación se puede transformar en rotatorio para operar algunas válvulas.

Posicionadores y elevadores de potencia (“boosters”)

El posicionador es un amplificador neumático – mecánico con retroalimentación que tiene una alta ganancia (de 1 a 100).

Hay otro dispositivo auxiliar que se emplea para mejorar el funcionamiento de ciertos tipos de elementos de control final, que es el reforzador o relevador piloto. El reforzador es un amplificador de alimentación directa y potencia neumática.

Válvulas alimentadoras de sólidos

Los actuadores de posición lineal y las válvulas de control que se describieron con anterioridad, se emplean primordialmente para el control de flujo de fluidos (líquidos o gases). Hay otras clases de equipos que se necesitan para manejar la transferencia de materiales sólidos. El equipo con válvula de medición de sólidos en particular depende del volumen, la densidad, la forma especifica y el tamaño de los sólidos que se van a manejar.

Propulsores de velocidad variable

El motor de velocidad variable es un propulsor de velocidad variable de uso común. Este tipo de dispositivo puede ser un motor eléctrico universal con una fuente de voltaje ajustable o un motor eléctrico de c.a., que se alimenta por medio de una fuente de frecuencia ajustable. Para aplicaciones especiales, el motor de velocidad variable puede ser de tipo turbina de gas o aire, en donde la presión de la fuente se hace variar para cambiar de velocidad.

6.6.5 Función de transferencia de elementos de transporte

Elemento de tiempo muerto (retardo en el tiempo) e^-Ls

El elemento de tiempo muerto, denominado comúnmente demora distancia – velocidad, o verdadera demora de tiempo, se encuentra con frecuencia en los sistemas de procesos. Por ejemplo, si un elemento de medida de temperatura se localiza corriente debajo de un intercambiador de calor, ocurre una demora de tiempo antes que el fluido calentado que sale del intercambiador llegue al punto en el cual se mide la temperatura.

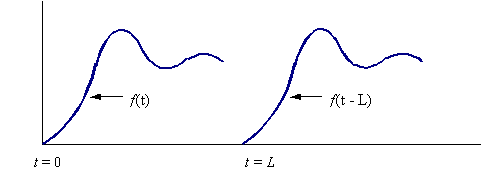
Fig. 6.25 Efecto del elemento de tiempo muerto

Si algún elemento del sistema produce un tiempo muerto de L unidades de tiempo, entonces cualquier entrada f(t) al elemento se reproducirá en la salida como f(t – L), al transformar esto al dominio de s, se tiene

L[f(t)] = F(s) = entrada

L[f(t – L)] = F(s) = salida

Fig. 6.26 Diagrama de bloques del elemento de tiempo muerto del proceso

6.6.5 Función de transferencia de elementos de transporte

Elemento de tiempo muerto (retardo en el tiempo) e^-Ls

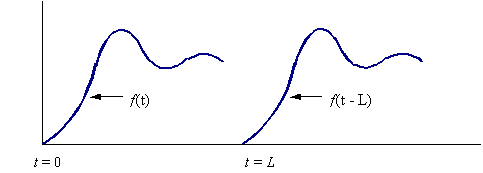
Fig. 6.25 Efecto del elemento de tiempo muerto

L[f(t)] = F(s) = entrada

L[f(t – L)] = F(s) = salida

Fig. 6.26 Diagrama de bloques del elemento de tiempo muerto del proceso

6.7 POLOS Y CEROS DE LA FUNCIÓN DE TRANSFERENCIA

Considerando un sistema descrito por la Ec. (6.1), tomando la trnsformada de Laplace y resolviendo para la razón de salida Y(s) a la entrada X(s), la función de transferencia del sistema G(s) será:

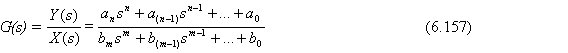
El denominador es un polinomio en s que es igual que en la ecuación característica del sistema. Recordando que la ecuación característica es obtenida a partir de la EDO homogénea, y haciendo el lado derecho de la Ec. (6.1) igual a cero.

Las raíces del denominador son denominadas los polos de la función de transferencia. Las raíces del numerador son denominados los ceros de la función de transferencia (estos valores de s hacen a la función de transferencia igual a cero). Factorizando numerador y denominador se tiene:

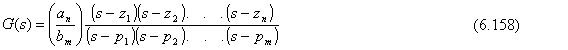
donde z_i = ceros de la función de transferencia

p_i = polos de la función de transferencia

Las raíces de la ecuación característica, las cuales son los polos de la función de transferencia, deben ser reales o deben ocurrir como pares de complejos conjugados. En adición, las partes reales de todos los polos deben ser negativas para que el sistema sea estable.

“Un sistema es estable si todos sus polos se ubican en el lado izquierdo del plano s”

La ubicación de los ceros de la función de transferencia no tienen ningún efecto sobre la estabilidad del sistema! Ellos ciertamente afectan la respuesta dinámica, pero no afectan la estabilidad

6.8 GANANCIAS AL ESTADO ESTACIONARIO

La ganancia al estado estacionario es la razón de la salida en el estado estacionario sobre la perturbación de entrada.

En el proceso de dos tanques con calentamiento dado en el Ejemplo 6.11, las dos funciones de transferencia son dadas por la Ec. (6.123). la ganancia al estado estacionario entre la temperatura de entrada T₀ y la salida T₁ se ha encontrado a ser 1 ^oF/^oF cuando s es establecido igual a cero. Esto dice que cuando cambia un grado en la temperatura de entrada variara la temperatura de salida un grado, lo cual es razonable. La ganancia al estado estacionario entre T₂ y el calor de entrada Q₁ es 1/2160 ^oF/Btu.min. Se debe tener cuidado en las unidades de la ganancia. Algunas veces se tienen unidades de ingeniería, como en este ejemplo, otras veces son usadas ganancias adimensionales.

6.9 FUNCIÓN DE TRANSFERENCIA DE LAZO ABIERTO Y FUNCIÓN DE TRANSFERENCIA DIRECTA

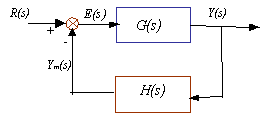
Al representar un sistema de control mediante un diagrama de bloques, se debe colocar en cada bloque la función de transferencia correspondiente al elemento del sistema. Así para el sistema de control de lazo cerrado mostrado en la Fig. 2.3

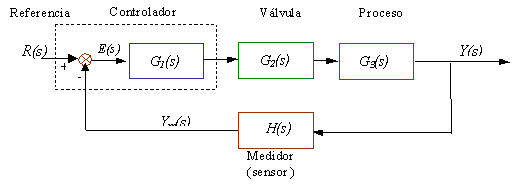
Fig. 6.27 Diagrama de bloques de un sistema de control de lazo cerrado

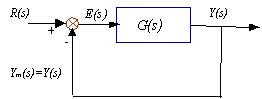
Como se vera más adelante, el diagrama de la Fig. 6.27 se puede reducir a la forma dada en la Fig. 6.28a y 6.28b.

(a)

(b)

Fig. 6.28 Sistema de lazo cerrado

a) H(s) ¹ 1

b) H(s) = 1

La salida Y(s) es alimentada nuevamente al punto de suma, donde se compara con la entrada de referencia R(s). La salida Y(s), se obtiene en este caso, multiplicando la función de transferencia G(s) por la entrada al bloque E(s).

Al inyectar nuevamente la salida al punto de suma para compararla con la entrada, es necesario convertir la forma de la señal de salida a la forma de la señal de entrada.

Por ejemplo, en un sistema de control de temperatura, la señal de salida es generalmente la temperatura controlada. La señal de salida, que tiene la dimensión de una temperatura, debe convertirse a una fuerza, posición o voltaje antes de compararla con la señal de entrada. Esta conversión lo realiza el elemento de retroalimentación (medidor), cuya función de transferencia es H(s).

La función del elemento de retroalimentación es modificar la salida antes de compararla con la entrada. En la mayoría de los casos el elemento de retroalimentación es un sensor que mide la salida del proceso. La salida del sensor se compara con la entrada (valor de referencia) y así se genera la señal de error. En este ejemplo la señal de retroalimentación que se envía de vuelta al punto de suma para su comparación con la entrada es Y_m(s) = H(s) Y(s).

Con referencia a la Fig. 6.28, la relación entre la señal de retroalimentación Y_m(s) y la señal de error actuante E(s), se denomina función de transferencia de lazo abierto. Es decir:

La relación entre la salida Y(s) y la señal de error actuante E(s) se denomina función de transferencia directa, de modo que:

Si la función de transferencia de retroalimentación H(s) es la unidad, la función de transferencia de lazo abierto y la función de transferencia directa son lo mismo

6.10 FUNCIÓN DE TRANSFERENCIA DE LAZO CERRADO

Para el sistema que se muestra en la Fig. 6.28, la salida Y(s) y la entrada R(s) están relacionadas como sigue:

Y(s) = G(s) E(s)

E(s) = R(s) – Y_m(s)

= R(s) – H(s)

Eliminando E(s) de ésta ecuación se tiene

Y(s) = G(s) R(s) – H(s) Y(s)

Usando MATLAB, la función de transferencia se evalúa de acuerdo a:

Para la Fig. 6.28a

Gs = feedback(G, H)

Para la Fig. 6.28b

Gs = feedback(G, 1)

La función de transferencia que relaciona Y(s) con R(s), se denomina función de transferencia de lazo cerrado. Esta función de transferencia relaciona la dinámica del sistema de lazo cerrado con la dinámica de los elementos de acción directa y los de la retroalimentación

De la Ec. (6.157) se obtiene Y(s) por:

Así la salida del sistema de lazo cerrado depende claramente tanto de la función de transferencia de lazo cerrado como de la naturaleza de la entrada

6.11 SISTEMAS SOMETIDOS A UNA PERTURBACIÓN DE CARGA

En la Fig. 6.29, se ve un sistema sometido a una perturbación. Cuando dos entradas (la señal de referencia y la perturbación) están presentes en un sistema lineal, cada entrada puede tratarse independientemente de la otra; y las salidas correspondientes se pueden sumar a cada una de las entradas individuales, para obtener la salida total. En el punto de suma se indica, ya sea por medio de un signo más o un signo menos, la forma en que cada entrada se introduce al sistema.

Considere el sistema que aparece en la Fig. 6.29. Al examinar el efecto de la perturbación N(s), se puede suponer que el sistema está inicialmente en reposo, con error cero, entonces se puede calcular la respuesta C_N(s) debida a la perturbación solamente.

Se puede hallar entonces que:

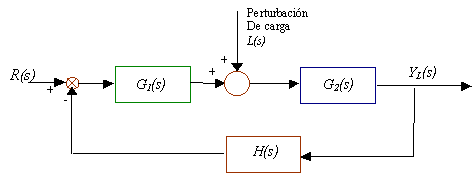
Fig. 6.29 Sistema de lazo cerrado sujeto a una perturbación

Por otro lado, considerando la respuesta a la entrada de referencia R(s), se puede suponer que la perturbación es cero. Entonces es posible obtener la respuesta Y_R(s) a la entrada de referencia R(s) de:

La respuesta a la aplicación simultánea de la entrada de referencia y de la perturbación se puede obtener sumando las dos respuestas individuales. En otras palabras, la respuesta Y(s) debida a la aplicación simultánea de la entrada de referencia R(s) y la perturbación L(s) está dada por

Y(s) = Y_R(s) + Y_L(s)

Ejemplo 6.15

Ecuación característica de lazo abierto para perturbación de carga

a) general

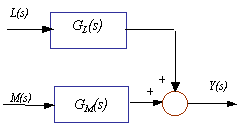
b) Ejemplo

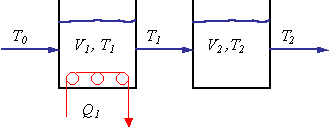
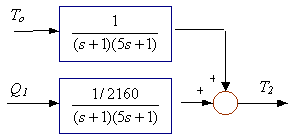
Fig. 6.30 Proceso de lazo abierto

Considerar el sistema general de lazo abierto mostrado en la Fig. 6.30. La carga variable L(s) ingresa a través de una función de transferencia de lazo abierto del proceso G_L(s). La variable manipulada M(s) ingresa a través de una función de transferencia del proceso de lazo abierto G_M(s). La variable controlada Y(s) es la suma de los efectos de la variable manipulada y la carga variable. Recordar que si trabajamos en el dominio de Laplace se aplica el principio de superposición.

La Fig. 6.30b muestra un ejemplo específico: el proceso de dos tanques con calentamiento discutido en el Ejemplo 6.11. La carga variable es la temperatura de entrada T_o. La variable manipulada es la entrada de calor al primer tanque Q₁. las dos funciones de transferencia G_L(s) y G_M(s) fueron discutida en el Ejemplo 6.11

La dinámica de este sistema de lazo abierto depende de las raíces de la ecuación característica, es decir las raíces del polinomio en el denominador de las funciones de transferencia del denominador. Si todas las raíces caen en el lado izquierdo del plano s, el sistema de lazo abierto es estable. Para los dos tanques con calentamiento del ejemplo mostrado en la Fig. 6.30b, los polos de las funciones de transferencia de lazo abierto son s = 1 y s = – 1/5, así el sistema de lazo abierto es estable.

Notar que la función de transferencia G_L(s) para el proceso de dos tanques con calentamiento tiene una ganancia de estado estacionario que tiene las unidades de ^oF/^oF. La función de transferencia G_M(s) tiene una ganancia con unidades de ^oF/Btu/min.

Ejemplo 6.16

Ecuación característica y funciones de transferencia de lazo cerrado para perturbación de carga

Ahora colocaremos un controlador de retroalimentación sobre el proceso, como muestra la Fig. 6.31a. La variable controlada es convertida en una señal de medición de

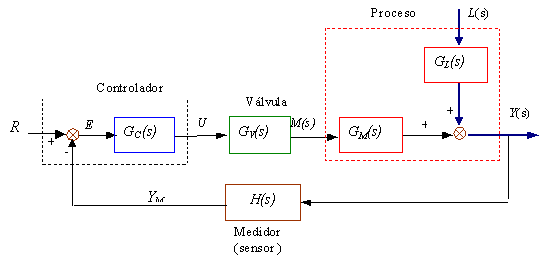
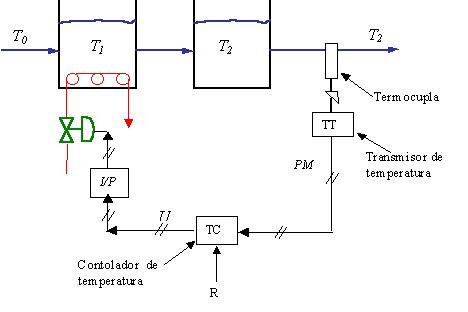
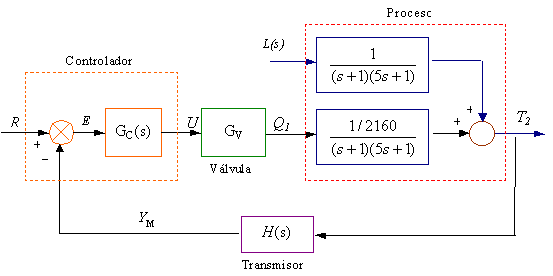
Fig. 6.31 Sistema de lazo cerrado

proceso Y_M por el elemento sensor/transmisor H(s). El controlador de retroalimentación compara la señal de Y_M con la señal de setpoint deseada R, alimentando la señal de error E a través de un controlador de retroalimentación cuya función de transferencia es G_C(s) y produce una señal del controlador U. La señal proveniente del controlador cambia la posición de la válvula de control la cual varía el flujo de la variable manipulada M

La Fig. 6.31b da una representación del sistema de control de retroalimentación y un diagrama de bloques para el proceso de dos tanques con calentamiento con un controlador. Usaremos un sistema analógico electrónico con señales de control de 4 a 20 mA. El sensor de temperatura tiene un rango de 100 ^oF, así la función de transferencia H (despreciando cualquier dinámica en la medición de temperatura) es

La señal de salida del controlador P va a un transductor I/P que convierte 4 a 20 mA a una señal de presión de aire 3 a 15 psig para mover la válvula de control a través de la cual se adiciona vapor al proceso.

Ahora asumiremos que la válvula tiene una característica lineal y pasa suficiente vapor para adicionar 500 000 Btu/min al liquido en el tanque cuando la válvula esta completamente abierta. Entonces la función de transferencia entre Q₁ y U (juntando la función de transferencia para el transductor I/P y la válvula de control) es

mirando el diagrama de bloques en la Fig. 6.31a, podemos ver que la salida Y(s) está dada por:

Y = G_L(s) L + G_M(s) M (6.168)

Pero en este sistema de lazo cerrado, M(s) está relacionada a Y(s):

M = G_V(s)U = G_V(s)G_C(s)E = G_V(s)G_C(s) ( R – Y_M)

M = G_V(s)G_C(s) ( R – H(s) Y ) (6.169)

Combinando las Ecs. (6.168) y (6.169)

Y = G_L(s)L + G_M(s) G_V(s) G_C(s) ( R – H(s) Y )

[1 + G_M(s) G_V(s) G_C(s) H(s) ] Y = G_L(s) L + G_M(s) G_V(s) G_C(s) R

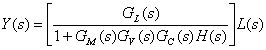
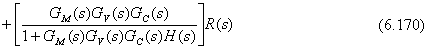
La Ec. (6.170) da las funciones de transferencia describiendo el sistema de lazo cerrado, así, estas son las funciones de transferencia de lazo cerrado. Las dos entradas son la carga L(s) y el setpoint R(s). La variable controlada es Y(s). Notar que los denominadores de ambas funciones de transferencia son idénticos.

Ejemplo 6.17

Las funciones de transferencia para el proceso de dos tanques calentados pueden ser calculadas a partir de las funciones de transferencia del proceso de lazo abierto y la función de transferencia del controlador de retroalimentación. Nosotros seleccionamos un controlador proporcional, de tal manera que G_C(s) = K_c.

Notar que las dimensiones de la ganancia de este controlador son mA/mA, esto es, la ganancia es adimensional. El controlador toma un miliamperio de la señal (Y_M) y envía una señal de un miliamperio (U)

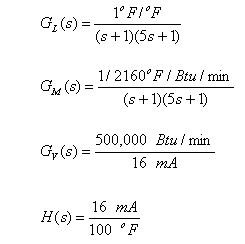
La función de transferencia de lazo cerrado para cambios en la carga es:

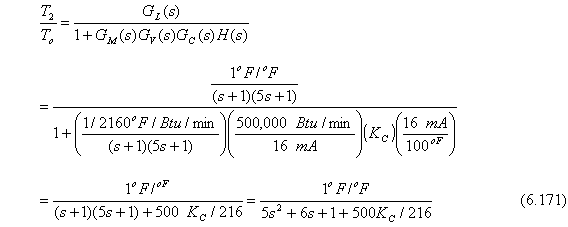
La función de transferencia de lazo cerrado para cambios en el setpoint es

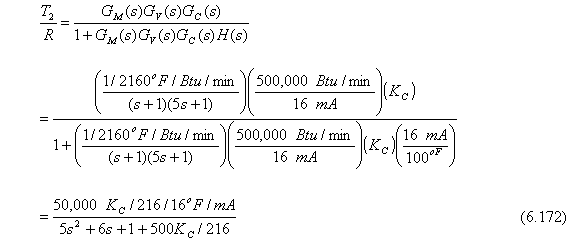
Si vemos las funciones de transferencia entre Y_M y R, debemos multiplicar la primera por H.

Notar que los denominadores de estas funciones de transferencia son idénticos. Notar también que la ganancia de estado estacionario de la servo función de transferencia de lazo cerrado Y_M/R no es la unidad; es decir, es un estado estacionario fuera del valor deseado (offset). Esto se debe al controlador proporcional. Nosotros podemos calcular la razón Y_M/R en el estado estacionario igualando s a cero en la Ec. (6.173)

La Ec. (6.174) muestra que mientras más pequeña es la ganancia, mas pequeño es el offset.

Como la ecuación característica de cualquier sistema (lazo abierto o lazo cerrado) es el denominador de la función de transferencia que lo describe, la ecuación característica para este sistema es:

Esta ecuación muestra que la dinámica de lazo cerrado depende de las funciones de transferencia de lazo abierto (G_M, G_V y H) y de la función de transferencia del controlador de retroalimentación G_C. La Ec. (6.175) se aplica para sistemas de simple entrada- simple salida (SISO). Nosotros derivaremos las ecuaciones características para otros sistemas en los siguientes capítulos.

La primera función de transferencia en le Ec. (6.170) relaciona la variable controlada a la carga variable. Esta es la función de transferencia reguladora de lazo cerrado. La segunda función de transferencia de lazo cerrado en la Ec. (6.170) relaciona la variable controlada al setpoint. Esta es denominada servo función de transferencia de lazo cerrado.

Normalmente nosotros diseñamos el controlador de retroalimentación G_C(s) para dar algún desempeño de lazo cerrado deseado. Por ejemplo, debemos especificar un deseado coeficiente de amortiguamiento de lazo cerrado.

Es de gran utilidad considerar la situación ideal. Si podríamos diseñar un controlador ideal fuera de cualquier consideración para la realización física, cuales deberían ser las funciones de transferencia reguladora y servo de lazo cerrado?. Claramente, desearíamos que una perturbación en la carga no tenga efecto sobre la variable controlada. Así, la función de transferencia reguladora de lazo cerrado es cero. Para cambios en el setpoint, nos gustaría que la variable controlada siguiera al setpoint en todo instante. Así, la servo función de transferencia ideal es la unidad.

Si vemos la Ec. (6.170) veremos que se pueden conseguir las dos situaciones si podemos simplemente hacer a G_c(s) infinitamente grande. Esto podría hacer al primer término cero y al segundo término la unidad. Sin embargo como se verá en el Cáp. 9, las limitaciones de estabilidad nos impiden conseguir esta situación ideal.

En lugar de considerar las funciones de transferencia del proceso, transmisor y válvula separadamente, es conveniente combinarlas a todas ellas en una sola función de transferencia.

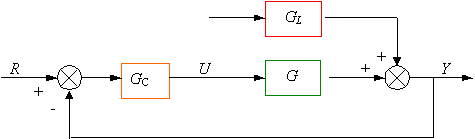
Fig. 6.32 Lazo de retroalimentación simplificado

Por consiguiente, el diagrama de lazo cerrado, mostrado en la Fig. 6.32 es mas simple. La ecuación que describe este sistema de lazo cerrado es:

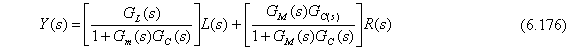
Estas son la ecuaciones que usaremos en algunos casos debido a que es más conveniente. Tener en cuenta que la función de transferencia G_M(s) en la Ec. (6.176) es una combinación de las funciones de transferencia del proceso, transmisor, y la válvula. La ecuación característica de lazo cerrado es:

6.12 OPERACIÓN PARA ANALISIS DE SISTEMAS DE CONTROL

Convencionalmente para el diseño de sistema de control, se somete el sistema a variaciones del setpoint (R) y determinar si la variable controlada sigue a los valores del setpoint y en que tiempo alcanza estos valores.

En consecuencia para esta caso la función de tranfernecia reguladora se hace cero, por lo que los sistemas dados en las Fig. 6.31 y 6.32 se transforman en:

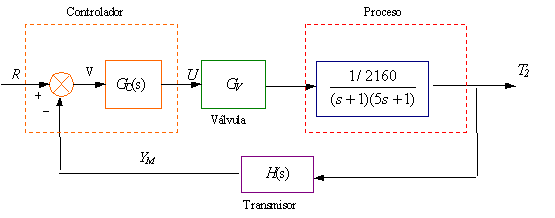
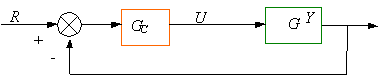
Fig. 6.33 Diagrama de bloques para operación servo para dos tanques con calentamiento a) Total b) Simplificado

Esta será la forma de representación que usaremos en la mayoría de nuestros análisis de sistemas de control.