Los sistemas dinámicos tuvieron sus inicios en sistemas de diferencias y en ecuaciones diferenciales (Forrester 1980). Un sistema objetivo, es descrito usando un sistema de ecuaciones, de las cuales se derivan los estados futuros de ese sistema desde el estado actual. Son representados por atributos llamados “Niveles y Tasas” actuando como ecuaciones en diferencia con puntos equidistantes en el tiempo.
Una típica ecuación en diferencias tiene la forma:
xt+1 = f(xt ; v) (4.1)
Donde xt+1 es el estado del sistema objetivo en el tiempo “t+1”, el cual depende del estado en el tiempo “t” y de un parámetro “v”. Usualmente la función f es continua.
Una típica ecuación diferencial tiene la forma:
dx/dt = g(x(t); v) (4.2)
Donde dx/dt es el cambio de estado del sistema objetivo en un periodo corto de tiempo dt. Estos cambios dependen de “t” y de “v”.
4.1 MODELO PARA EL CO2 TOTAL
La acumulación creciente de CO2 en la atmósfera constituye un experimento a gran escala en el ambiente de la Tierra con repercusiones de largo plazo desconocidas. El balance radiacional entre la Tierra y espacio puede ser afectado significativamente por las acumulaciones del CO2, por ejemplo, el llamado “efecto invernadero “, que puede producir incrementos significativos en la temperatura atmosférica de la Tierra. El incremento en la temperatura, a su vez, puede producir a su vez mayores cambios en el ambiente, por ejemplo, fusión de hielo polar, clima severo, efectos adversos en la agricultura.
Así, los estudios cuantitativos de acumulación del CO2 son esenciales para elucidar y entender cuáles factores contribuyen a la acumulación del CO2. Un modelo matemático introductorio de los factores que contribuyen a la generación del CO2 y la acumulación son desarrollados en el subsiguiente ejemplo. El modelo puede ser usado, por ejemplo, para estudiar el efecto del creciente quemado de combustible fósil y la destrucción de áreas forestales. El modelo incluye un componente de clima. Éste es un modelo pequeño de términos, en el que la transferencia de carbón hacia y desde el sedimento y el carbonato (ambos procesos de transporte de largo plazo) quedan excluidos.
La estructura del modelo es ilustrada en la Figura 4.1 y consiste de cinco reservorios interconectados:
- Atmósfera
- La Biosfera Terrestre
- Superficie del océano
- Carbón del suelo y detritus
- Profundidad del océano
Los rectángulos representan los reservorios, cada uno con un valor inicial (en giga toneladas de carbón). Los flujos son representados por las flechas grandes con los círculos adjuntos a la presente. Estos están en unidades de giga toneladas/año. Los círculos simples, conocido como “convertidores”, tienen constantes numéricas o fórmulas algebraicas representando funciones matemáticas específicas.
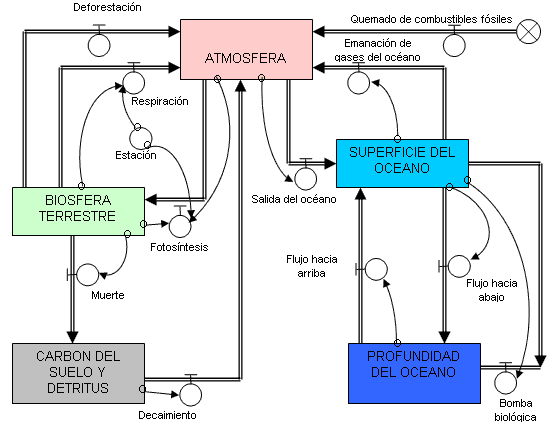
Figura. 4.1 Diagrama de flujo para la simulación del CO2 total en STELLA
Nuestro interés es evaluar la cantidad de carbón en los reservorios en cualquier período de tiempo dado sobre el tiempo de simulación, específicamente la cantidad de carbón atmosférico presente. Los flujos representan los diversos procesos que afectan la cantidad de carbón que podrían ser depositados o removidos de un reservorio. Incluidos en los flujos están las ecuaciones para calcular fotosíntesis estacional, emanaciones desde el océano, la respiración, la muerte, la descomposición, y otros.
Ecuaciones diferenciales
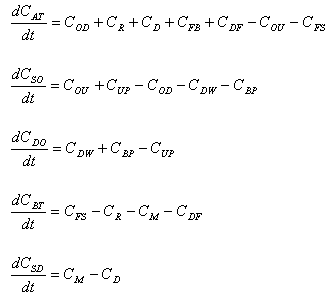
Ecuaciones algebraicas
![]()
CUP = CDO * 0.002
CDW = CSO* 0.002
CBP = 6.76 + CSO / 700
COD = CSO / 20
Est = 1+ (cos(2*pi*(t +0.125)))
CR = CBT * 0.1* Est
CFS = (CBT * 0.1483+ CAT /700) * Est
CM = 0.05* CBT
CD = 0.021* CSD + CAT / 750
AtmCO2 = CAT /2
Donde:
CAT = carbón total en la atmósfera
COD = carbón emanada desde el océano
CR = carbón debido a la respiración de los seres vivos
CD = carbón debido a descomposición de seres muertos
CFB = carbón debido al quemado de combustibles fósiles
CDF = carbón debido a la deforestación de los bosques
COU = carbón tomado por el océano
CFS = carbón usado en la fotosíntesis
CSO = carbón en la superficie del océano
CUP = carbón desde el fondo del océano
CBT = carbón en la biosfera terrestre
CDW = carbón hacia el fondo del océano
CBP = carbón en plantas marinas
CDO = carbón en el fondo del océano
CM = carbón en los seres muertos
CSD = carbón en la superficie terrestre
Est = variación estacional
AtmCO2 = CO2 en la atmósfera
t = tiempo
pi = 3.1416
Las condiciones iniciales son tomadas para el año base (1970) en giga toneladas:
Valor inicial de carbón en la atmósfera (reservorio): CATo = 700
Valor inicial de carbón en la superficie del océano (reservorio): CSOo = 700
Valor inicial de carbón en la biosfera terrestre (reservorio): CBTo = 550
Valor inicial de carbón en el fondo del océano (Reservorio): CDOo = 35000
Valor inicial de carbón en la superficie terrestre (reservorio): CSDo = 1200
Parámetros que dependen de la actividad del hombre:
Deforestación: 2
Flujo de combustibles fósiles: 5
Las ecuaciones básicas representan las matemáticas requeridas para representar el transporte “natural” de carbón a través de este sistema. Para añadir una variable antropogénica para la mezcla, incluimos la adición de carbón al reservorio de la atmósfera a través del quemado de combustibles fósiles (estimado a ser 5 gigatons al año) y el efecto de deforestación (2 gigatons adicionales moviéndose de la biosfera terrestre a la atmósfera). En este modelo, usted puede experimentar con el cambiar de estas dos variables (junto con la mayor parte de las demás) en el modelo.
Al correr el modelo obtiene como resultado un gráfico de la cantidad de CO2 en la atmósfera
4.2 SIMULACIÓN DE DINÁMICA DE POBLACIONES BIOLÓGICAS: UN ENFOQUE DE DINÁMICA DE SISTEMAS
La administración de los recursos renovables ha estado fundamentada en el concepto de máximo rendimiento sustentable, según el cual el inventario de los recursos biológicos no puede sobreexplotarse sin una pérdida final de productividad. Este concepto se basa en esquemas de crecimiento biológico. En este punto se presentan algunos modelos de crecimiento bajo el enfoque de dinámica de sistemas, lo cual permite estudiarlos mediante simulación y análisis de sensibilidad. Se presentan los principios del modelamiento de ecosistemas, los modelos clásicos de crecimiento (exponencial y logístico) y en anexo, los fundamentos de la dinámica de sistemas.
4.2.1 Modelos de Crecimiento Poblacional
El manejo de los recursos naturales renovables se ha basado en el concepto de máximo rendimiento sustentable, según el cual el inventario de recursos no puede sobreexplotarse sin una pérdida final de productividad. Este concepto se fundamenta en un modelo de crecimiento biológico, en el cual se plantea que a cualquier nivel poblacional, menor que un cierto nivel K (indicativo de la capacidad de carga ambiental o nivel de saturación), existe una sobreproducción que puede ser cosechada indefinidamente sin alterar el nivel de inventario (Clark, 1976).
Ahora bien, si no se cosecha ese superávit de producción, entonces se genera un aumento en el nivel de inventario, que finalmente alcanza la capacidad de carga ambiental K, punto en el cual se anula la sobreproducción. Como el exceso de producción se iguala al rendimiento sustentable para cada nivel de población, entonces el punto de máximo rendimiento sustentable se alcanza en el nivel poblacional No, para el cual dicho exceso de producción es máximo (coincide con el punto en el cual se maximiza la tasa de crecimiento poblacional).
Los modelos que explican la explotación de los recursos biológicos se basan en una estructura de ecuaciones diferenciales del tipo:
dY/dt = F(Y)-h(t) (4.3)
donde
Yt : representa el tamaño de la población en t,
F(Y) : indica la tasa de crecimiento poblacional
h(t) : representa la tasa de cosecha (“harvesting rate”).
El comportamiento dinámico de la población depende de la relación entre ambas tasas F(Y) y h(t).
El nivel poblacional declina, sí F(Y)< h(t), pues dY/dt< 0. Mientras que, si F(Y)= h(t), la población se mantiene en un nivel constante, pues dY/dt = 0; ello significa que la tasa natural de crecimiento F(Y) se iguala con el valor del rendimiento sustentable que puede ser para poder diseñar modelos de planificación de manejo de los recursos renovables es fundamental especificar los modelos de crecimiento poblacional adecuados en cada caso.
Uno de los hechos fundamentales de la dinámica poblacional es el potencial de crecimiento exponencial (Caswell, 1988), popularizado por Malthus, quien en 1798 en su obra Essay on the Principle of Population, estableció que una población sin restricciones se incrementaría geométricamente. Ahora bien, las poblaciones no pueden mantener indefinidamente este crecimiento exponencial, planteándose los modelos de crecimiento poblacional restringido o modelos logísticos, deducidos por Pierre Verhulst en 1838. Luego siguieron extensiones a los casos de competencia entre especies diferentes, y de interacción tipo predador-presa (Lotka, 1924; Volterra, 1926; Gause, 1934; Kostitzin, 1939).
Basándose en los trabajos de Lotka, se desarrollaron modelos que consideran a la población clasificada por grupos de edad, para así resolver la limitación de los modelos que tratan a todos los individuos de la población en forma idéntica.
Todas las teorías ecológicas respecto a las poblaciones y a las comunidades tienen que ver, de una u otra manera, con sus tamaños, cómo crecen o decrecen, si presentan un crecimiento estable o si fluctúan, cómo responden a los cambios ambientales y cómo influyen en los cambios en el ambiente de otras poblaciones.
4.2.2 Modelo de crecimiento exponencial
El tamaño de las poblaciones de seres vivos se mantiene en equilibrio, oscilando más o menos ampliamente en torno a un valor medio, en función de variables como la natalidad o la mortalidad, que a su vez dependen de relaciones más complejas con otras poblaciones de otras especies, variaciones en las condiciones ambientales, etc.
El crecimiento de una población, es decir el incremento en el número de individuos que la componen en cada generación depende de la tasa de natalidad, característica de cada especie y variable en función de ciertos factores ambientales, y del número de individuos reproductores de que se parte. Esta tasa de natalidad TN se expresa en tanto por uno. Según esta aproximación tan simple, en una generación el número inicial de individuos N0 se verá incrementado en N0·TN:
N1 = N0 + N0·TN = N0·(1 + TN) (4.4)
Al mismo tiempo, ocurre que cierto número de individuos mueren. La proporción de muertes respecto al total es la tasa de mortalidad TM (también en tanto por uno). Según esta aproximación, en una generación el número inicial de individuos N0 se verá disminuida en N0·TM:
N1 = N0 – N0·TM = N0·(1 – TM) (4.5)
Luego, considerando al mismo tiempo las tasas de natalidad y mortalidad, el número total de individuos después de un primer periodo de tiempo será:
N1 = N0 + N0·TN – N0·TM (4.6)
N1 = N0 (1+ TN – TM) (4.7)
La acción conjunta de TN y TM determinan el incremento real de N0. La diferencia entre TN y TM es la tasa intrínseca de crecimiento de una población, cuyo valor máximo se denomina potencial biótico (r), el cual es característico de cada especie:
r = TN – TM (4.8)
Teniendo en cuenta ambos factores, tenemos que el número de individuos presentes en la población en la siguiente generación será:
N1 = N0·(1 + r) (4.9)
en la siguiente generación tendremos:
N2 = N1 (1 + r) = N0 (1 + r) (1 + r) = N0 (1 + r)2 (4.10)
Y generalizando:
Nt = N0 (1 + r)t (4.11)
Si TN > TM, significa que la natalidad supera a la mortalidad, r será mayor que 0 y la población tiende a crecer. En estas condiciones y si no existen limitaciones de otro tipo, la población crece de manera exponencial. El siguiente ejemplo muestra este tipo de crecimiento partiendo de N0 = 6 y r = 0,1, o sea una tasa del 10%
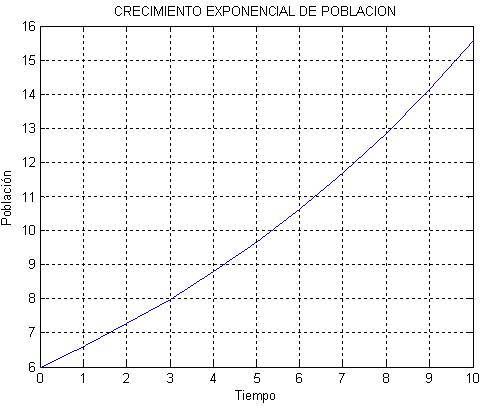
Figura. 4.3 Crecimiento exponencial de población
El proceso descrito es determinístico, es decir, se asume que en un instante dt, cada individuo produce la fracción rdt de nuevos individuos. (El correspondiente modelo estocástico asume que en el intervalo dt un individuo produce un descendiente con una probabilidad rdt, y hay una probabilidad 1– rdt de no generar descendientes.)
Con este modelo puede estudiarse el comportamiento de una población bajo los siguientes supuestos o restricciones:
- El modelo considera sólo los nacimientos.
- La tasa reproductiva es igual para cada individuo y constante durante toda la edad reproductiva.
- No hay interacción entre los individuos.
- El espacio y los recursos que consumen los organismos son ilimitados.
Sin embargo, este tipo de crecimiento sólo es posible en circunstancias muy específicas, por ejemplo cuando una especie coloniza un nuevo espacio y no hay restricciones en los recursos ni competencia por ellos, tal como ocurre en un cultivo bacteriano recién inoculado durante los primeros momentos de su crecimiento. Algunas especies siguen este modelo de crecimiento siguiendo ciclos de explosión demográfica seguidos por elevados índices de mortalidad, por ejemplo al comienzo de la estación reproductora. Presentan curvas de crecimiento en forma de dientes de sierra:
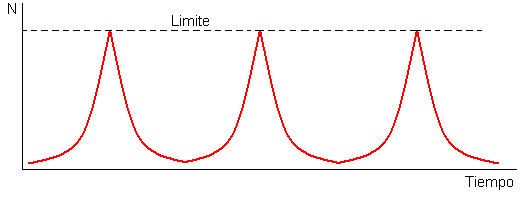
Figura. 4.4 Modelo de población con ciclos d explosión demográfica
Dinámica del crecimiento exponencial
Pare representar la dinámica del modelo de crecimiento exponencial se requiere expresar el modelo mediante una ecuación diferencial. Para esto, partiendo de la Ecuación. (4.6), el incremento en el número de individuos ∆N para un periodo de tiempo ∆t, cuando ∆t→0 es:
dN/dt = (TN – TM )N (4.12)
Donde N representa el nivel poblacional en cada instante t, TN y TM representan la natalidad y la mortalidad según las tasas porcentuales de natalidad y mortalidad n y m respectivamente; ambas variables, TN y TM son variables de flujo (representan el cambio en la población N por unidad de tiempo t). Las tasas porcentuales de natalidad y mortalidad son parámetros que permanecen constantes durante el período de análisis.
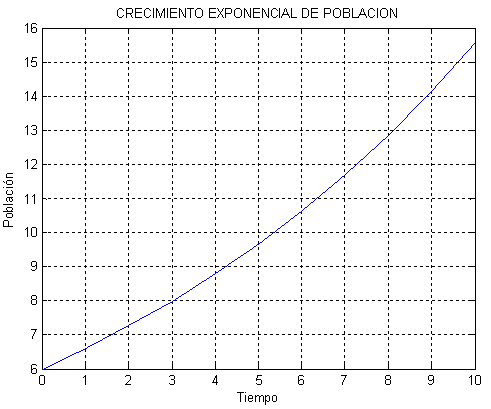
Figura. 4.5 Crecimiento exponencial de Población
Al potencial biótico, como capacidad de una especie para reproducirse en condiciones ideales, se opone una serie de factores que, en conjunto, constituyen la resistencia ambiental, la cual establece un límite al crecimiento de las poblaciones. En especies con un comportamiento como el descrito estos factores suelen ser independientes de la densidad de población, como variaciones climáticas, en la cantidad de alimento disponible, etc.
4.2.3 Modelo de crecimiento logístico
Malthus, ya a fines del siglo XVIII, planteó el modelo de crecimiento exponencial precedente y concluyó que, como la población aumentaba geométricamente y los recursos sólo aritméticamente, había un límite natural al crecimiento de la población (Malthus, 1798).
Medio siglo después, Darwin creó el concepto “Severe Struggle for Existente” para explicar este fenómeno. Es decir, en condiciones ideales una población debía crecer exponencialmente, pero la existencia de otras especies y lo limitado de los recursos, generaba en ellas una severa competencia que llamó “lucha por la existencia”.
No todas las especies estaban igualmente capacitadas, y creó el concepto de aptitud de adaptación (“fitness”) para expresar la calidad de la relación entre cada organismo y su ambiente (conjunto de todos los factores externos que pueden influenciar a los organismos durante su vida). Esta medida de la calidad de relación entre el organismo y su ambiente estaba determinada por factores tales como: fertilidad, habilidad para conseguir alimento, habilidad para evitar peligros, etc. Darwin, además postuló que estas características, ese “fitness”, era hereditario, transmitiéndose a los descendientes, de generación en generación. Luego, si los individuos de una población tienen más “fitness” que los individuos de otra población, los primeros podrían aumentar su número más rápidamente, teniendo una mejor oportunidad para sobrevivir y procrear individuos como ellos; habría así una selección natural de los organismos.
La objeción a la ecuación de crecimiento exponencial es que, para r>0, la población se incrementa explosivamente, mientras que si r < 0 la población decrece hacia la extinción, fluctuando alrededor de un valor finito, si r = 0; pero es evidente que nunca alcanza valores infinitos. Usualmente se denomina resistencia ambiental al conjunto de factores ambientales que limitan el crecimiento de una población (reducción en la tasa de natalidad, incremento en la tasa de mortalidad). El tamaño máximo (expresado en individuos, biomasa, energía, etc.) de una población permitido por un cierto ambiente se conoce como capacidad de carga de ese ambiente. La capacidad de carga varía, no sólo en función de las variables ambientales, sino también con relación a los atributos de la población considerada.
Representando este tamaño máximo por K (corresponde a la N máxima para un ambiente dado), se deduce el modelo logístico básico, en el que se establece una tasa de crecimiento poblacional en función de la densidad de la población, es decir:
F(N)= dN/dt = r(N)N (4.13)
Siendo:
r(N) = ro(1-N/K) (4.14)
Esto genera la ecuación logística, que se expresa como:
dN/dt = roN[1-(N/K)] (4.15)
La relación anterior puede descomponerse de la siguiente manera,
dN/dt = roN-(ro/K)N2 = roN-bN2 (4.16)
Como se observa, el lado derecho de la ecuación está formado por dos términos: el primero, roN, que representa la tendencia de la población a crecer exponencialmente a una tasa ro , y el término bN2, cuyo papel es reflejar la reducción poblacional causada por conflictos entre individuos de la misma especie (efecto competencia).
Cuando r se hace dependiente del tamaño de la población (y por tanto del tiempo) su valor cambia con las fluctuaciones de la población. De manera que r toma el valor r(t) en el intervalo (t ; t+dt) y esto define la ecuación logística.
dN/dt = (r-bN)N (4.17)
El razonamiento que sustenta esta ecuación es simple: la población se incrementa, pero a medida que aumenta la densidad poblacional, disminuye la tasa de crecimiento hasta detenerse al llegar a una densidad máxima definida. Ahora, en el modelo logístico, la tasa de crecimiento exponencial r, ha sido reemplazada por (r – bN), una función lineal de N, siendo b el parámetro que expresa en qué grado la densidad poblacional hace disminuir la tasa de crecimiento de la población. Cuando esta tasa de crecimiento se hace cero, la población cesa de crecer y el tamaño N de la población representa la capacidad de carga del ambiente (N = K).
El modelo logístico se basa en los siguientes supuestos:
- La población tiene una estructura estable por edades.
- La tasa de variación (dN/dt) decrece en una cantidad constante y en forma instantánea.
- El ambiente no se modifica y la capacidad de carga K es constante.
- La congestión afecta igualmente a todos los individuos.
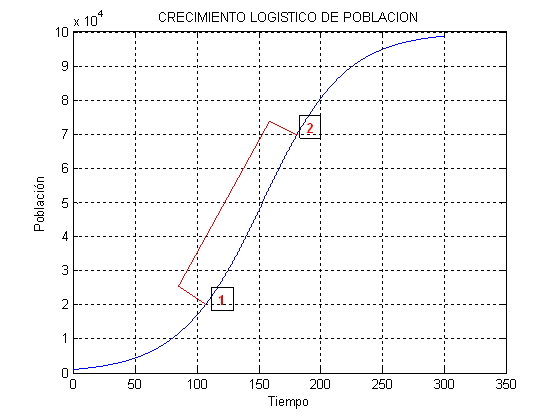
Figura 4.6 Modelo de crecimiento logístico de población
La tasa de natalidad es primero muy elevada y luego va siendo menor hasta igualarse a la de mortalidad cuando la población alcanza el límite de carga. Por encima de éste, la tasa de mortalidad supera la de natalidad e impide que la población crezca. Sin embargo, es frecuente que tras un período de crecimiento rápido este ajuste tarde en ocurrir lo suficiente como para que la población supere el nivel K momentáneamente, tras lo cual se produce una elevada mortalidad y caída de la población. Puede ocurrir que el valor de N oscile en torno a K hasta alcanzar el equilibrio.
El máximo crecimiento de la población y la máxima producción se da mientras se mantiene la etapa de crecimiento exponencial, antes que los factores dependientes de la densidad tomen importancia limitando el crecimiento. En la siguiente figura, corresponde al segmento comprendido entre los puntos 1 y 2.
La explotación de los ecosistemas por el hombre, ya hablemos de agricultura, ganadería o pesca, consiste en extraer biomasa manteniendo el ecosistema inmaduro, evitando que progrese la sucesión y el consumo respiratorio suponga una menor producción neta. Desde el punto de vista de la demografía se trataría de mantener la población en ese segmento 1-2 de crecimiento exponencial, evitando que el aumento de la densidad haga decrecer la producción. Pero la sobreexplotación significa extraer más deprisa de lo que puede crecer la población, se reducirá su densidad a un nivel inferior al de producción óptima (antes del punto 1 de la gráfica). El buscar el máximo beneficio en el menor plazo posible puede conducir a reducir los niveles de la población objeto de explotación por debajo de ese umbral crítico que permita la recuperación de la misma.
1. Formulando relaciones empíricas, basadas en datos de poblaciones específicas, en las que se definen las tasas de crecimiento o decrecimiento en función de la densidad poblacional; por ejemplo, puede definirse la fracción de mortalidad como una función directa del tamaño poblacional: m = f(N), f’ > 0; el punto en el cual la fracción de decrecimiento supera a la fracción de crecimiento, se denomina punto de inflexión de la curva (punto en el que se produce el máximo crecimiento neto); allí, el proceso de feedback positivo asociado con el crecimiento de la población, comienza a perder su dominancia, a favor del proceso de feedback negativo relacionado con el decrecimiento poblacional; la población continúa creciendo, pero a una tasa neta menor y cada vez más baja, hasta que se detiene en el estado estacionario (punto en el que N=K).
2. Especificando relaciones causales entre la población y el sustrato alimenticio (la tasa de crecimiento depende directamente de los recursos disponibles para la población). Suponiendo que la tasa de reproducción r es proporcional a la concentración de nutrientes o alimento C (unidades de nutriente) , r = kC, y que el incremento de la población en una unidad requiere el consumo de b unidades de nutriente, entonces el sistema población-nutriente puede representarse por el siguiente par de ecuaciones:
Ecuación de la población:
dN/dt = rNt = kCNt (4.18)
Ecuación del nutriente:
dC/dt = -b(dN/dt) = -bkCNt (4.19)
donde:
N = unidades de población
C = unidades de nutriente
b = unidades de nutriente consumido /unidad de población incrementada
r = tasa de crecimiento
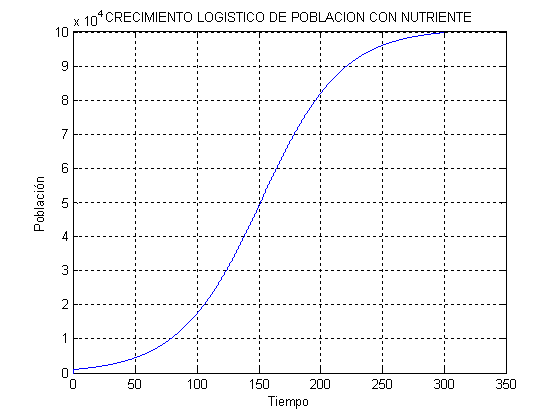
Figura. 4.7 Modelo de crecimiento logístico con nutriente |
4.2.4 Modelo de crecimiento con interacción de especies
Los modelos poblacionales con interacción de especies que se consideran en este texto son del tipo predador-presa; específicamente se analizan los siguientes modelos:
a. Modelo general predador-presa.
Uno de los modelos más simples usados para investigar la dinámica de población predador-presa es el modelo de Lotka-Volterra. Aún cuando no es usualmente preciso para sistemas intrincados, es a menudo utilizado como una base para modelar la mayoría de sistemas complejos. El modelo de Lotka-Volterra es un sistema de dos ecuaciones diferenciales: una que describe la población de presas y otra que describe la población del predador. Hay algunas suposiciones críticas, principalmente son:
- La presa tiene recursos ilimitados.
- La única amenaza de la presa es el depredador.
- El depredador es un especialista; es decir, el único suministro de comida del depredador es la presa.
- El crecimiento del depredador depende de la presa que atrapa.
Los supuestos para el modelamiento matemático son los siguientes:
- La presa (Pres) crece sin límites, en ausencia de los predadores (P); si Pred=0, entonces dPres/dt = aPres.
- Los predadores mueren en ausencia de las presas; si Pres=0, entonces dPred/dt = 0.
- La natalidad de los predadores está directamente relacionada con el consumo de las presas b(Pred*Pres) .
- El consumo de presas por parte de los predadores es proporcional al número de contactos entre las dos poblaciones –b(Pred*Pres).
Sobre la base de estos supuestos se construye el modelo básico predador-presa, el cual consta de dos ecuaciones diferenciales:
dPres/dt = aPres – b(Pred*Pres) (4.20)
dPred/dt = – c Pred + d (Pred*Pres) (4.21)
Donde:
a = tasa de crecimiento de la presa
b = eficiencia de habilidad del depredador para capturar presa
c = la tasa de mortalidad del depredador
d = la tasa de crecimiento del depredador
Estas ecuaciones representan el cambio en las poblaciones de predador y presa a medida que pasa el tiempo. Notar que dPres/ dt tiene un término Pred, y por otro lado, dPred /dt tiene un término Pres. Esto se debe a que las dos poblaciones están interconectadas; el tamaño de una población tiene un efecto sobre el tamaño de la otra población.
La cantidad Pres*Pred indica la cantidad de dos organismos encontrados uno al otro. Cuando cualquiera de las poblaciones es baja, la velocidad de encuentro es baja. Cuando las poblaciones son altas, también la velocidad de encuentro es alta.
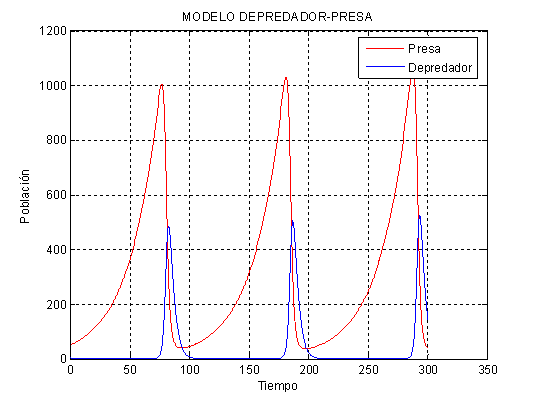
Figura. 4.8 Modelo predador – presa
Como se puede ver en la Figura 4.10., hay órbitas cerradas rodeando el punto crítico (a/b, c/d ) (40, 300) que implica que las soluciones son periódicas con el tiempo y que el máximo de cada población es interactuando el uno del otro. Hay un punto de silla en (0, 0) que representa la ausencia de ambas poblaciones. El punto de silla muestra que si hay la presa y no hay ninguno de los depredadores la presa crecerá (ver el sentido de las flechas en el eje x). Por otro lado, si hay depredadores y ninguna presa para comer, entonces se extinguirán por la ausencia de comida (ver el sentido de las flechas en el eje y), lo cuál es obvio en la vida real.
b. Modelo predador-presa con crecimiento logístico:
Uno de los problemas con el modelo de Lotka-Volterra inicialmente propuesto, ecuaciones (4.20 ) y (4.21) es el hecho de que a falta de depredadores, la presa crecerá continuamente. Éste no es el caso ya que mientras la presa continúa creciendo, el espacio y los recursos se acabarán eventualmente, limitando por consiguiente el crecimiento de la población de presas. Para manipular este caso, el sistema depredador-presa puede ser modificado a:
dPres/d t = a (1–Pres/K) Pres – b(Pres*Pred) (4.22)
dPred/d t = – c Pred + d (Pred*Pres) (4.23)
donde K es la máxima cantidad de presas que puede existir en el modelo. Por lo tanto si K = 5, entonces si una pequeña cantidad de presas fuesen adicionadas a un sistema sin depredadores la presa podría crecer hasta 5 a medida que t®∞ en oposición al crecimiento de l numero de presas hasta ∞ cuando t®∞. Analizando la ecuación (4.22), si la población de presas es mayor que la capacidad de acarreo, el término (1 – Pres/K) será negativo asegurando que la población de presas disminuirá.
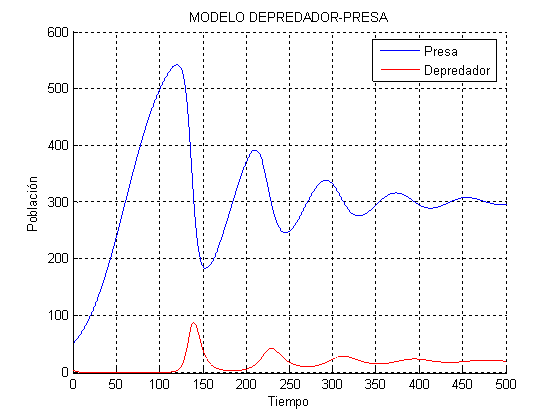
Figura. 4.11 Modelo predador – presa con crecimiento logístico de presa
En la Figura. 4.11 se muestra el diagrama correspondiente a este modelo: se tienen dos variables de nivel, (población presa (Pres) y predador (Pred)), con sus correspondientes flujos de natalidad y mortalidad. La interacción de las dos especies, produce un comportamiento oscilatorio convergente debido al crecimiento logístico de la población Presa.
4.3 CONTAMINACIÓN DE UN LAGO
Este ejemplo es acerca del uso de ecuaciones diferenciales para modelar contaminación en un lago debido al vertido de contaminantes.
Modelar contaminación de un lago puede ser complicado, porque hay muchos factores diferentes que pueden ser tomados en consideración. Usaremos un modelo simplificado, y consideraremos sólo a unos cuantos factores básicos, que describimos a continuación.
4.3.1 Modeamiento del Sistema
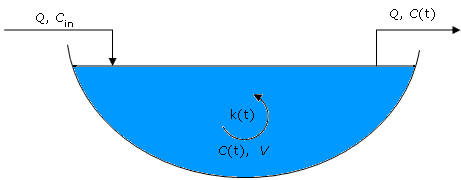
Figura 4.14. Lago como un modelo de flujo bien mezclado
Donde:
Q
: Flujo volumétrico a través del lago
V
: Volumen del lago
k (t )
: Coeficiente de velocidad de reacción del contaminante
C (t )
: Concentración del contaminante tanto dentro como en la salida del lago
Cin(t )
: Concentración del contaminante entrando al lago
Aplicando el balance de masa de un contaminante al estado no estacionario, se tiene:
Acumulación = Entrada – Salida – Desaparición por reacción
![]()
La Ecuación. (4.24) es el modelo matemático para la concentración de contaminación en un lago. El volumen V de agua en el lago – se asume – a ser constante. El contaminante es llevado al lago por un flujo entrante de agua a una tasa Q (volumen por unidad de tiempo) y con una concentración Cin (masa por unidad de volumen). Hay un flujo de salida correspondiente a una tasa Q desde el lago, y esta salida tiene la misma concentración C de contaminante que en el lago (como es el caso para un lago de mezcla completa). C y Cin dependerán del tiempo. Tenemos en cuenta una reacción química, con constante de velocidad k, en la cual el contaminante en el lago se descompone en otras sustancias que no son de ninguna preocupación.
Aquí hay algunos escenarios para lo que ocurre en el lago, conjuntamente con las elecciones que deberemos hacer para simular cada escenario. Seleccionamos “No Reacción [k(t ) = 0] ” si la reacción de descomposición es insignificante, y escogemos “Constante de velocidad de reacción de Primer Orden [k(t ) =k, para la constante k]” si se tienen cualesquiera de los dos casos en las simulaciones.
4.3.2 Modelamiento del sistema con SIMULINK
SIMULINK es un entorno gráfico para usar con MATLAB en modelado, simulación y análisis de sistemas dinámicos. Simulink puede simular cualquier sistema que pueda ser definido por ecuaciones diferenciales continuas y ecuaciones diferenciales discretas. Esto significa que se puede modelar sistemas continuos en el tiempo, discretos en el tiempo o sistemas híbridos.
![]()
Q
: Flujo volumétrico a través del lago: 10
V
: Volumen del lago : 898,800 gal
k (t )
: Coeficiente de velocidad de reacción del contaminante
C (t )
: Concentración del contaminante tanto dentro como en la salida del lago
Cin(t )
: Concentración del contaminante entrando al lago 1.0
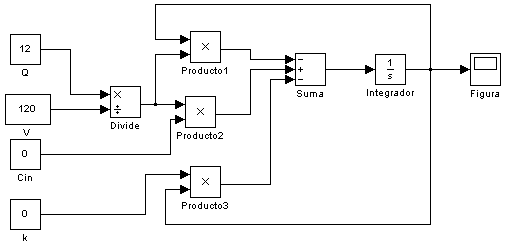
Figura. 4.15 Modelo en SIMULINK de la Ecuación. 4.25
4.3.3 Caso 1: Vertido instantáneo de contaminantes
Un pescador participaba de su actividad favorita (la pesca, por supuesto! ) en su lugar favorito el lago local, donde la única corriente de salida va a un río.
Desafortunadamente, se quedo sin combustible y cuando llevaba el combustible de repuesto para su motor fuera de borda, tropezó y dejó caer el tanque por la borda. Como consecuencia, 10 galones de gasolina casi instantáneamente fueron distribuidos en el lago que contiene 898,800 galones y del cual salen 89,880 galones /día de agua pura hacia un río.
Cuando el pescador contactó las autoridades apropiadas, y cuando las autoridades desconectan el flujo de salida del lago, han pasado cuatro días. Por lo que las autoridades están preocupadas por la cantidad de gasolina que ha salido del lago y cortaron el flujo de salida del lago mientras se toman las acciones respectivas. Si se escaparón 1 000 000 mg o más de gasolina, entonces la concentración en la corriente saliente será demasiado alta para los estándares aceptables y medidas muy costosas tendrán que ser tomadas para limpiar la corriente. Si escapó menos de eso, entonces sólo tienen que preocuparse por limpiar el lago.
¿Cuánto de gasolina todavía se queda en el lago, y hará que la corriente saliente tenga que ser remediada?
Solución
Para encontrar la respuesta, primero deberíamos decidirnos cómo debemos modelar la entrada (el derramamiento de gasolina). Si lo modelamos como
- Un Impulso,
- Un escalón
- O una función sinusoidal
La solución correcta en este caso es la función de impulso, ya que toda la gasolina entra en el reservorio al mismo tiempo. En muchas aplicaciones, puede ser más difícil decidir cuál modelo usar, pero en este caso debería ser claro que un modelo de impulso es más conveniente.
También necesitamos decidir qué clase de reacción ocurre. (En este ejemplo, consideramos solamente k = 0). Suponemos que la gasolina no reacciona con el agua, sedimento o microorganismos en el
Tiempo final (tf). Una cantidad que necesitamos conocer es el tiempo final tf. En el enunciado del problema, se dice que 10 galones fueron derramados en el tiempo t = 0 (para nuestro propósito). También sabemos que las autoridades fueron avisadas 4 días después para tomar las acciones respectivas, por lo que:
Tiempo final tf = 4 días
El caudal (Q). Otra cantidad que necesitamos saber es la tasa de flujo, Q. Esto no fue dado en el enunciado del problema, pero podemos pretender que tal información estaría disponible. Supongamos que encontramos que a la hora que el flujo fue recortado, el lago tenía una de salida de 89,880 galones /día.
Si queremos mantener las unidades en términos de días y pies, cual deberá ser el caudal en términos de miles de pies3/día ? (Use: 1 pie3 = 7.49 galones.)
Solamente necesitamos convertir el caudal dado de 89 880 galones por día en miles de pies3/día. Por lo tanto:
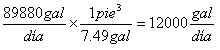
Caudal en miles de pies3/día=12
Volumen del lago. Si el lago tiene 898 000 galones, el volumen en miles de pies3 será:
![]()
Volumen en miles de pies3 = 120
Concentración inicial. Finalmente necesitamos conocer la concentración inicial de gasolina en el lago.
Si suponemos que la mezcla fue instantánea y completa, podemos encontrar la concentración inicial dividiendo la cantidad de gasolina derramada por el volumen del lago.
Sin embargo, queremos saber cuanto de masa ha escapado, no la concentración que permanece. El modelo calcula la concentración final dada la concentración inicial. Si queremos saber cuánto de masa ha escapado, necesitaremos multiplicar la concentración final por el volumen total del lago en razón a calcular cuanto de masa de contaminante permanece.
Datos:
Densidad de la gasolina:
800,000 mg/litro
Litros en un galón:
3.79 litros/galón
Volumen de agua en el lago:
898,800 galones
Volumen de gasolina derramada:
10 galones
Usando esta información, calculamos la concentración inicial de gasolina en el lago en mg/litro, de la manera siguiente:
(800 000 mg/litro)x(37.9 litrs/galón) = 30 320 000 mg de gasolina derramada.
(898 800 galones de agua)x(3.79 litros/galon) = 3 406 572 litros de agua
Luego:
(30 320 000 mg de gasolina)/( 3 406 572 litros de agua) = 8.9
C(0) = 8.9 mg/litro
Efectuando la simulación. Los parámetros para la simulación son:
Tiempo final (tf):
4 días
Volumen (V):
120 miles de ft3
Concentración Inicial (C0):
8.9 mg/litro
Caudal (Q):
12 miles de ft3/día
Al efectuar la simulación se tiene la respuesta dad en la Figura (4.13):
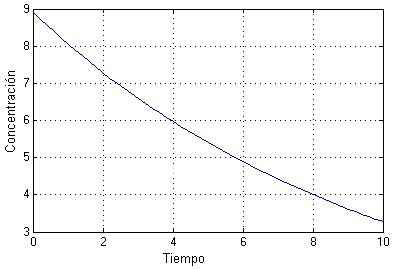
Figura 4.16. Solución del modelo SIMULINK
De la Figura 4.16, vemos que la concentración al cabo de 4 días es alrededor de 5.97 mg/litro.
Para calcular la cantidad de gasolina que permanece en el lago hacemos los siguientes cálculos:
Volumen del lago en litros:
(898 800 galones)(3.79 litros/galón) = 3 406 452 litros
Cantidad de gasolina que permanece en el lago:
(5,97 mg/litro) (3 406 452 litros = 20 340 000 mg.
La cantidad inicial fue 10 galones o 37,9 litros
La cantidad derramada fue de 30 320 000 mg.
Por lo que la cantidad de gasolina que ha salido del lago es:
30 320 000 – 20 340 000 = 9 980 000 mg.
Se han escapado más de lo aceptable, por lo que debe proceder la limpieza.
4.3.4. Caso2: Vertido continuo de contaminantes
Considerar un lago que contiene V litros de agua el cual está a % contaminado. Una alcantarilla se vacía en el lago a una tasa de S litros al día. El agua en la alcantarilla esta b% contaminado. Un río también se vacía en el lago en una tasa de R litros al día. El agua en el río está c % contaminado. El lago drena por otro río a razón de S +R litros al día lo cual hace que el volumen del lago permanezca constante, es decir, el volumen del lago está en estado estacionario. El problema luego es determinar el nivel de contaminación del medio ambiente en el lago después un año (o algún otro período de tiempo, por decir n días).
Los datos de muestra son: V = 1 000 000 000, a = 0.1, S = 30000, b = 10, R = 70 000, c = 0.5, n = 365.
Análisis
Para cualquier día dado
La contaminación inicial en el lago es (a / 100) V, litros
La contaminación que entra en el lago desde de la alcantarilla es (b / 100) S, litros
La contaminación que entra en el lago desde el primer río es (c / 100)R litros
Así, la contaminación total que desemboca en el lago es (bS + cR) /100.
La contaminación actual así se convierte en (aV + bS + cR) /100.
La contaminación que drena del lago en el segundo río equivale a la contaminación actual del lago.
Modelamiento Matemático:
Ahora, tenemos dos corrientes de estrada y una corriente de salida, por lo que la Ec. (4.25) se escribe como:
![]()
| V | : Volumen del lago : 1 000 000 000 litros |
| S | : Caudal de entrada de la alcantarilla: 30 000 litros/día |
| R | : Caudal de entrada del primer río: 70 000 litros/día |
| a | : Porcentaje de contaminantes del lago : 0.1 |
| b | : Porcentaje de contaminantes en la alcantarilla : 10 |
| c | Porcentaje de contaminantes en el río : 0.5 |
4.4 MODELOS PARA LA SIMULACIÓN DE UNIDADES DE PROCESO
4.4.1 Tanque dinámico
Uno de los principales problemas de contaminación en la industria se debe a los derrames de líquidos. Estos derrames pueden deberse a fallas en el sistema de control de nivel, rotura de las paredes del tanque o sobrepasar la capacidad del tanque.
Al diseñar un tanque y no se tiene un sistema de control de nivel, se debe determinar cuanto mas de flujo por encima de la capacidad actual puede soportar el tanque antes de que se presente un derrame.
Considerando el tanque mostrado en la Figura. 4.20
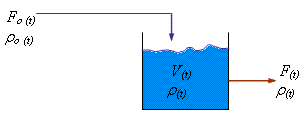
Figura. 4-20 Tanque perfectamente mezclado
Balance de materiales:
F0 ro – F r = velocidad de cambio de rV =d(rV)/dt

Balance de Momentum
La segunda Ley de movimiento de Newton dice que la fuerza es igual al producto de la masa por la aceleración para un sistema de masa constante M.
![]()
donde F = fuerza, N (lbf)
m = masa, Kg. (lbm)
gc = constante de conversión necesaria cuando se usan unidades Inglesas de
ingeniería, para mantener consistencia en las unidades = 32,2 lbm pie/lbf seg2
Esta es la relación básica, la cual es usada para la ecuación de movimiento para un sistema. En una forma más general, donde la masa puede variar con el tiempo,
![]()
donde vi = velocidad en la dirección i, m/s (pies/s)
Fji = j-ésima fuerza actuando en la dirección i
Asumiendo condiciones de flujo en pistón y de liquido incompresible, y por lo tanto todo el liquido se está moviendo a la misma velocidad, mas o menos similar a una varilla sólida. Si el flujo es turbulento esta no es una mala asunción.

La dirección de interés en este problema es la horizontal, ya que se asume que la tubería es horizontal. La fuerza actuando sobre el liquido en el extremo izquierdo de la tubería es la fuerza de presión hidráulica del liquido en el tanque
![]()
Las unidades de esta fuerza son N (lbf)
La única fuerza actuando en dirección opuesta, de derecha a izquierda y oponiéndose al flujo es la fuerza de fricción debido a la viscosidad del liquido. Si el flujo es turbulento, la fuerza de fricción será proporcional al cuadrado de la velocidad y la longitud de la tubería.
Fuerza de fricción = KF L v2 (4.34)
Reemplazando esta fuerza en la Ecuación. 4.29, tenemos

El signo de la fuerza de fricción es negativo debido a que actúa en la dirección opuesta al flujo. Hemos definido de izquierda a derecha la dirección positiva.
Las Ecuaciones. 4.33 y 4.36 representan el modelo matemático para el tanque al ENE.
Al Estado Estacionario
![]()
La Ecuación. (4.33) es una ecuación algebraica lineal simple la cual podemos usar para determinar la velocidad de salida (v) en función del nivel de líquido en el tanque (h), para lo cual hacemos la Ecuación. (4.33) explicita en v, obteniendo:

Con las Ecuaciones. (4.33) y (4.37) podemos evaluar las condiciones de operación al estado estacionario.
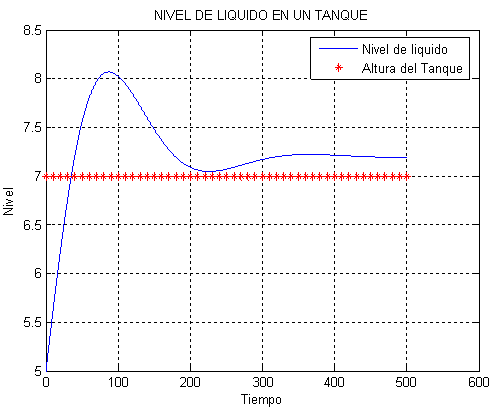
Figura. 4.21 Simulación de un tanque dinámico para un aumento en el caudal de entrada
Comentarios:
Del resultado de la simulación se observa lo siguiente:
- Cuando el tanque opera al estado estacionario con un caudal de entrada de 36.1545 pies3/min, el tanque alcanza un nivel de 5 pies.
- Si partiendo de estas condiciones de operación, se eleva repentinamente el caudal en 20% (36.1545*0.2 = 7.2309 pies3/min), el nivel de liquido sobrepasa el nivel del tanque produciéndose por lo tanto un derrame de liquido.
4.4.2 Tratamiento de efluentes
Una fábrica en construcción quiere descargar agua contaminada en un río. El límite legal para la concentración de contaminante entrando en el río es 5×10-4 g/m3. Este límite plantea un problema para el gerente técnico de la compañía Mr. Mamani, porque se sabe que la fábrica producirá una concentración de descarga variando entre 10-3 y 10-2 g/m3 (siempre por encima del límite legal). El asesor de la compañía Mr. Quispe, aconseja que un sistema biológico de tratamiento usando un tanque de mezcla completa de volumen 104 m3 reducirá la concentración de contaminante a un nivel aceptable.
MAMANI no confía en QUISPE, por lo que pregunta al experto de investigación y desarrollo de la compañía, Mr. SILVA, a contestar a las siguientes preguntas:
a) el esquema propuesto siempre surtirá efecto?
b) puede ser un sistema más realista usando dos tanques más pequeños?
El modelo de un tanque discutido en la lectura conduce al sistema de ecuaciones diferenciales:

Donde
Cf = concentración de contaminante procedente de la fábrica: g/m3
(10-3 < Cf < 10 -2)
B = concentraciones de microorganismos biológicos en el tanque en el tiempo t horas: g/m3
Q = caudal entrando y saliendo del tanque: 10 m3/hora
V = volumen del tanque: 104 m3
R1 = 0.1 m3/g.h
R2 = 1.2625 m3/g.h
D = 10-5
(R1, R2 y D son estimaciones empíricas de las constantes de velocidad para digestión del contaminante, crecimiento del organismo y mortalidad natural del organismo respectivamente)
Cleg = límite legal: 5×10-4 g/m3
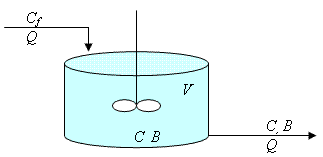
Figura. 4.22 Esquema del tanque de tratamiento biológico
Solución
a) Verificar que las dimensiones de las ecuaciones diferenciales sean correctas
b) Mostrar que en el estado estacionario donde dC/dt = dB/dt = 0 son posibles dos soluciones (Cs, Bs)
(i) Cs = Cf y Bs = 0 esto corresponde a una completa evacuación (lavado) del microorganismo desde el tanque
(ii) Cs = (D + Q/V)/R2 y Bs = Q(Cf – Cs)/(VCsR1)
Por lo que Cs < Cleg
c) Notar que el valor al estado estacionario Cs = (D + Q/V)/R2 es independiente de la concentración de contaminante desde la fábrica. Sin embargo un salto (elevación) de Cf producirá una elevación transitoria con C(t) > Cleg. En el largo plazo por supuesto que el sistema regresaría a Cs = (D + Q/V)/R2
Hacer V un parámetro de entrada.
Asumir que los valores iniciales de C y B están dados por sus valores al estado estacionario para el caso Cf = 10-3. Notar que los valores iniciales dependen del volumen V, así es que deberían calcularse en el programa usando las fórmulas para Cs y Bs, usando el valor de 10-3 para Cf.
Considerar el caso extremo donde a t=0, la concentración de contaminante desde la fabrica cambia a Cf =10-2 , y es mantenido indefinidamente en este valor.
Debido a ste cambio, es de esperarse que la concentración de contaminante en el tanque C(t) y la concentración de microorganismos B(t) se elevarán en respuesta a este cambio en la salida de la fábrica, después caerán a un nuevo estado estacionario.
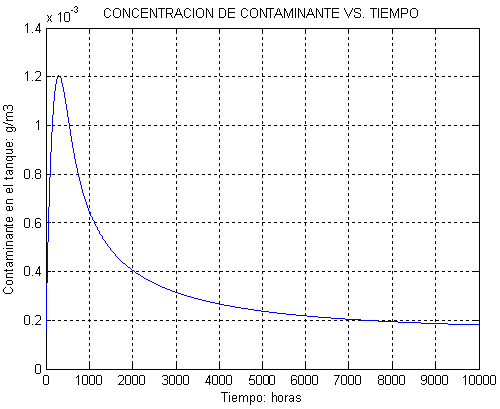
Figura 4.23 Concentración de contaminante
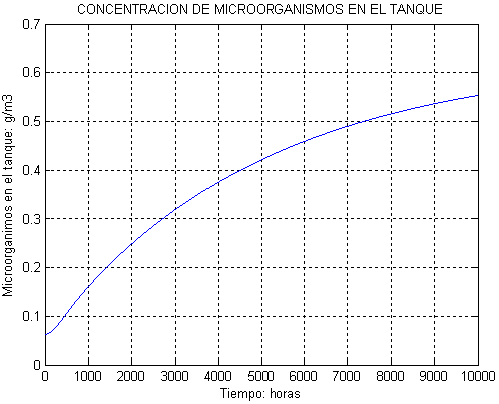
Figura. 4.24 Concentración de microorganismos
Con un tanque de 104 m3, la concentración máxima de contaminante es 1.2×10-3 g/m3, la cual es mucho mayor que el límite legal permitido Cleg = 5×10-4 g/m3.
Simular C(t) y B(t) para diferentes volúmenes de tanque V>Vmin , determinar la concentración máxima alcanzada y evaluar cual volumen es el adecuado.
a) Un solo tanque de tratamiento de los contaminantes dados anteriormente es definitivamente inadecuado. Mr. SILVA por lo tanto propone construir un sistema de dos tanques como muestra la Figura 4.21:
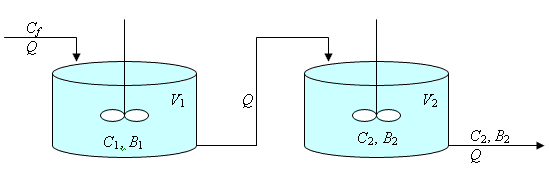
Figura. 4.25 Planta de tratamiento con dos tanques
Donde Cj y Bj son las concentraciones de contaminante y microorganismos y Vi es el volumen en el tanque j (j = 1; 2). Q = 10 m3/hora es el flujo entrando y saliendo de cada tanque Cf es la concentración de entrada de contaminante saliendo de la fábrica.
Usar los mismos valores dados anteriormente para R1, R2, etc
Las Ecuaciones diferenciales para C1, B1, C2, y B2 bajo la sunción de mezcla completa son:
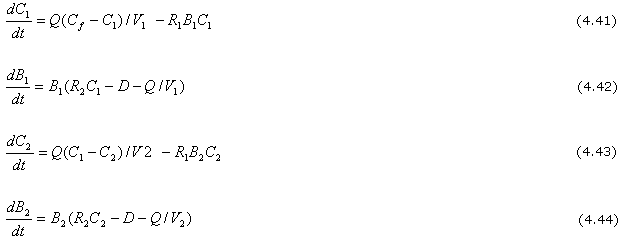
(i) Suponer V1 = 10000 y que las concentraciones iniciales son:
C1(0) = C2(0) = 0.0, B1(0) = B2(0) = 0.005. Notar que C2(0) está por debajo del límite legal Cleg = 0.0005.
Escribir un programa en MATLAB que simule C1(t), B1(t), C2(t) y B2(t) con Cf = 0:001 para diferentes valores de entrada de V2 y C1(0), C2(0), B1(0) y B2(0).
La salida C1(t), B1(t), C2(t), B2(t) y Cleg para un periodo de tiempo de hasta 50 000 horas
Confirme que los valores al estado estacionario (es decir los valores independientes del tiempo) para el caso donde V1 = V2 = 10000, son C1 = 0.00080, C2 = 0.00049, B1 = 0.0025 y B2 = 0.0064.
Variando B1(0) y B2(0) muestre que este resultado al estado estacionario es independiente de la concentración inicial de microorganismo. Sin embargo el caso donde la concentración inicial de microorganismo es cero es diferente. Explicar que pasa en este caso especial.
(ii) Ahora podemos ocuparnos del caso donde el nivel de salida de contaminación de la fábrica es aumentado de Cf = 0.001 a Cf = 0.01. Veremos el comportamiento transitorio para el caso Cf = 0.01 con resultados de salida sobre un tiempo total de 5000 horas. Use un cálculo de prueba y error para estimar el valor mínimo de V2, de tal manera que C2 < 2xCleg para cualquier t. Simular el sistema para esta elección de V2.
Por simplicidad asuma que las condiciones iniciales para este caso son las dadas como la salida de la parte c(i) anterior, es decir V1 = 10000, C1(0) = 0.00080, C2(0) = 0.00049, B1(0) = 0.0025 y B2(0) = 0.0064, aún cuando en la práctica desde luego estos valores cambiarán con diferente V2.
4.4.3 Reactor “batch” para minimización de residuos
Una planta química de manufactura tiene pensado en una modificación del producto que resultará en un cambio en el carácter de los residuos. De significancia es la anticipada presencia de fenol, un producto químico orgánico que no ha sido tratado por las facilidades de tratamiento de residuos de la compañía. Consecuentemente, la habilidad de las facilidades existentes para “tratar” fenol está en cuestión. En razón a predecir el desempeño del reactor existente, es necesaria información de cinética y dispersión.
Los datos cinéticos de reacción han sido recolectados la destrucción química de fenol a través de experimentos en un reactor batch (Tabla 4.1).
Tabla 4.1. Datos cinéticos de Reactor Batch.
| Tiempo
(min.) |
Fenol
(mg/L) |
| 0 | 100 |
| 10 | 55 |
| 20 | 22 |
| 30 | 8 |
| 40 | 5 |
| 60 | 0.82 |
| 80 | 0.15 |
El flujo del residuo que contiene fenol es proyectado para ser 0.45 MGD con una anticipada concentración de fenol de 95 mg/L. El reactor (un proceso químico de oxidación) tiene un volumen total de líquido de 25,000 gal. (L = 35 ft., W = 12 ft., H = 8 ft.). Un análisis de dispersión del reactor ha sido realizado inyectando un impulso de material poco reactivo en la corriente de alimentación al reactor. La tasa de flujo fue monitoreada durante el estudio de dispersión y se determinó a ser 0.45 MGD. Los datos del trazador en el reactor son presentados en la (Tabla 4.2).
El límite permitido de descarga de fenol ha sido determinado en 0.1 mg/L por la junta reguladora estatal. Estime la concentración de fenol en efluente basado en la información disponible. Determine qué podría hacerse para alcanzar el límite de descarga. Se podría mantener el reactor existente debido a las razones económicas obvias. Sin embargo, cualquier opción de diseño razonable puede considerarse. Justifique su recomendación final del diseño. Muestre todos los cálculos en una forma clara y sucinta. Declare todas las suposiciones que usted hace en el proceso del diseño. Deberá asumir que la relación cinética (Tabla 4.1) es fija y no puede ser alterada. Esto es, los datos cinéticos de la reacción representa condiciones óptimas.
Tabla 4.2. Datos de dispersión del reactor de escala de laboratorio.
| t
(min.) |
Conc.
(mg/L) |
| 0 | 0 |
| 44.75 | 0.23 |
| 46 | 0.32 |
| 49.62 | 0.36 |
| 48 | 0.82 |
| 48.5 | 1.24 |
| 49 | 2.15 |
| 49.33 | 2.61 |
| 50 | 2.98 |
| 50.75 | 2.93 |
| 51.67 | 2.98 |
| 52.75 | 2.89 |
| 54 | 2.84 |
| 56 | 2.89 |
| 58 | 2.84 |
| 60 | 2.52 |
| 62 | 2.52 |
| 64 | 1.92 |
| 66 | 1.79 |
| 68 | 1.6 |
| 70 | 1.33 |
| 75 | 1.28 |
| 79 | 1.14 |
| 83 | 1.1 |
| 98 | 0.41 |
| 113 | 0.39 |
| 128 | 0.27 |
Solución
La solución se basa en la utilización de la información cinética (Tabla 4.1) y la información de dispersión (Tabla 4.2) para estimar el desempeño del reactor actual y para desarrollar alternativas para mejorar el proceso de tratamiento. El acercamiento a la solución es presentado a continuación.
- Determinar orden y velocidad de reacción
- Determinar la varianza normalizada (σ2θ=σ2 /tbar2)
- Determinar el número (N) de CSTR’s en serie que simule la dispersión calculada (σ2θ= 1/N)
- Determinar la concentración actual del efluente del reactor
- Desarrollar modificaciones alternativas de diseño del reactor.
a. Constante de velocidad y Orden de reacción. La constante de velocidad y el orden son determinados usando los datos dados en la Tabla 4.1 del enunciado del problema. La expresión general de velocidad (Ecuación. 4.35) es aplicada en el análisis del proceso.
![]()
donde
k = constante de velocidad de reacción
n = orden de reacción
Después de asumir un orden de reacción, la Ecuación 4.45 es integrada y algebraicamente manipulada de tal manera que se desarrolla una relación general dada por una línea recta (Ecuación. 4.46).
y = mx + b (4.46)
Por ejemplo, si asumimos n = 0, se aplica la siguiente solución

La Ecuación (4.47) es la relación de una línea recta e indica que si los datos de rección son verdaderamente de orden cero, una gráfica de Ct vs. T deberá resultar en una línea recta. Sin embargo, si los datos no corresponden a una línea recta, debe asumirse otro orden y repetir los cálculos.
Por ejemplo, asumiendo n = 1, se tiene la siguiente solución a la ecuación:
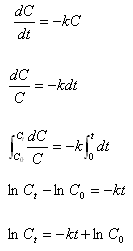
El resultado de efectuar estos cálculos sobre los datos cinéticos dados en la Tabla 4.1 son mostrados en la Figura. 4.26:
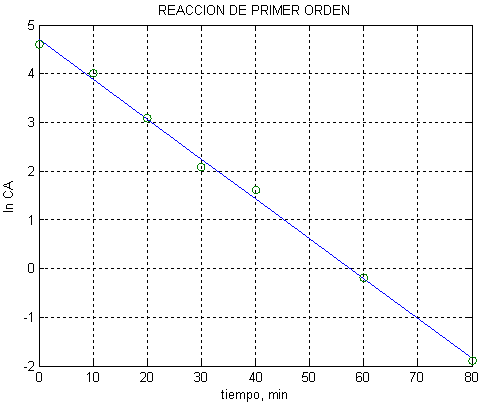
Figura 4.26 ln(C) vs. tiempo para los datos dados en la Tabla 4.1.
Los datos en la Figura. 4.26 indican que para la asunción de primer orden (n = 1) ln(C) vs t caen en una linea recta. La velocidad de reacción es por lo tanto de primer orden contendiente igual a k = 0.08 min-1.
b. Determinación de la Dispersión del Reactor. Ahora conocemos que la destrucción del fenol es de primer orden. El siguiente paso es utilizar los datos del trazador en el reactor para determinar el actual HRT y el número de CSTR en serie que simula la dispersión del reactor. Como los datos del trazador en el reactor son obtenidos en incrementos desiguales de tiempo, las siguientes ecuaciones tienen aplicación.

Resolviendo las Ecuaciones. (4.48) y (4.50) se obtienen los siguientes valores:
t = 74.9 min
s2 = 657.92
σ2θ= 0.117
N = 8.52 » 9
La siguiente ecuación es luego usada para efectuar la simulación mostrada en la Figura. 4.27.

Aunque no es absolutamente necesario para graficar la simulación, ofrece una manera de comprobación para ver qué tan adecuadamente la simulación hace juego con los datos reales y es altamente recomendable
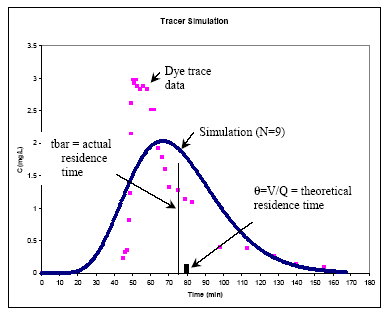
Figura 4.27. La posición de (t) y CSTR en serie, simulación basada en incrementos iguales de tiempo y corresponden a la aplicación de las ecuaciones 4.48 y 4.49.
Predicción de Ce para el reactor actual. Hasta aca esta todo bien, pero, ahora qué que hacemos para determinar la concentración efluente para nuestro reactor de escala?. Aplicamos la ecuación 4.52, la expresión para predecir desarrollada a partir de un balance de masa alrededor de una serie de N CSTR’s de igual volumen.
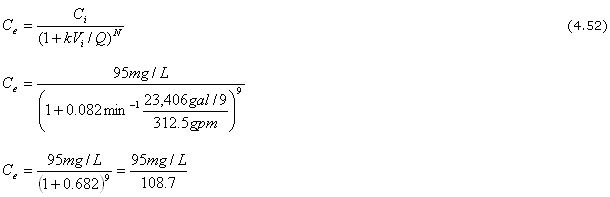
Ce = 0.88 mg/L
Deberá notarse que el valor para V/Q, está basado en el volumen efectivo (Veff), donde
Veff = qeff Q (4.53)
y
qeff = t
o
Veff = 74.9 min x (312.5 gpm)
Veff = 23406 gal
Alternativas del reactor. Basado en la concentración de descarga calculada (Ce) de 0.88 mg/L, el reactor existente no alcanza los criterios estatales de 0.1 mg/L. Las siguientes modificaciones alternativas del reactor se consideran aquí. No incluyen todas las alternativas posibles, sólo dos representativas.
- Adicionar un reactor en el efluente para el reactor existente.
- Adicionar un reactor en paralelo igual al reactor existente.
Otra alternativa atractiva sería ir aguas arriba y ver si el residuo de fenol podría ser minimizado (reducir el flujo y/o la concentración). Esta aproximación siempre debería ser considerada como es a menudo más costoso y efectivo para minimizar el contaminante en la fuente.
Para determinar el volumen requerido del reactor para cada alternativa, debe hacerse una suposición relacionando las características de dispersión del reactor nuevo. Éste es un resultado del impacto obvio de N, así definida por la dispersión del reactor, sobre los requerimientos de volumen del reactor (ver ecuación 4.52). La selección de N finalmente debería ser comprobada para su validez antes de seguir con la implementación a escala total. Las características de dispersión del reactor podrían ser comprobadas en el sistema existente sobre un rango de flujos para probar la suposición en caso de la alternativa 2. Las características de dispersión del reactor nuevo estaban especificadas en el diseño y el logro del nivel deseado de dispersión se basaría en experiencia con configuraciones diferentes del reactor.
Representaciones esquemáticas simplificadas de las dos alternativas son mostradas en la Figura. 4.28.
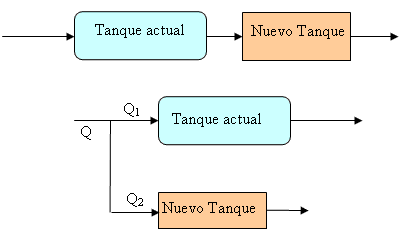
Figura 4.28. Representaciones esquemáticas de las dos alternativas de configuración del reactor.
El requerimiento de volumen de reactor en cada una de las dos alternativas, puede determinarse usando la Ecuación. 4.52 en combinación con las asunciones de dispersión. Las asunciones de diseño aplicadas aquí son:
- N = 9 para el tanque existente y nuevo
- La concentración de descarga para los propósitos del diseño es 0.07 mg/L. Esto resulta en un coeficiente de seguridad que es incorporado en los cálculos de volumen.
Diseño de reactores en serie. La manipulación de la Ecuación. 4.52 da como resultado la Ecuación. 4.54
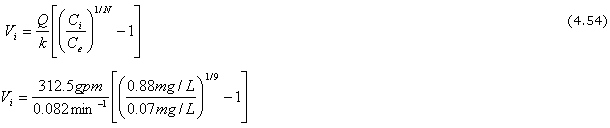
Vi = 3811 gal [1.325 – 1]
Vi = 1238 gal
V = NVi
V = (9)1238 = 11,141 gal
Diseño de reactor en paralelo. La determinación del volumen mínimo requerido para el reactor nuevo a ser colocado en paralelo requiere la determinación del flujo necesario en el reactor existente para alcanzar una Ce de 0.07 mg/L. Este flujo (Q1) es usado para definir el flujo (Q2) al nuevo reactor mediante un balance de materiales (flujo).
Q1 = 213.3[2.23 – 1]-1
Q1 = 173.4 gpm
Q2 = Q – Q1 = 312.5 – 173.4 = 139 gpm
El volumen del nuevo tanque es entonces calculado usando la Ecuación. 4.54
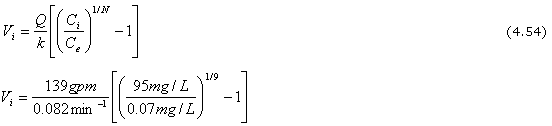
Vi = 1695 gal [2.23 – 1]
Vi = 2083 gal
V = NVi
V = (9)2083 = 18,745 gal
El nuevo tanque para la opción de tanques en serie es aproximadamente 40 % más pequeño que el arreglo de tanque en paralelo. La adición de un tanque a la descarga del tanque existente podría ser por lo tanto considerada.
4.5 MODELAMIENTO USANDO ECUACIONES DE DIFERENCIA
4.5.1 Contaminación de un río
Considere un río que ha sido contaminado río arriba. La concentración (cantidad por el volumen) decaerá y se dispersará corriente abajo. Nos gustaría predecir en cualquier punto con el tiempo y el espacio la concentración del contaminante. El modelo de la concentración tendrá la forma y(t+Δt) = Ay(t) + b. La contaminación del medio ambiente en corrientes, lagos y acuíferos clandestinos se ha convertido en una preocupación muy común y seria. Es importante para poder entender las repercusiones de posible contaminación del medio ambiente y poder hacer predicciones precisas concerniente a los “derramamientos” y la política “ambiental” futura.
Quizá, el modelo más simple para contaminante químico se basa en descomposición química, y un modelo el es similar a descomposición radiactiva. Un modelo continuo es ut = – du donde d es la velocidad de descomposición química. Una versión discreta es uk +1= uk + Δt (- d ) uk, y para la estabilidad esto requiere 1 – Δt d > 0.
Aquí introduciremos un segundo modelo donde el contaminante cambia de posición porque está en una corriente. Asumimos que la concentración dependerá de ambos espacio y tiempo. La variable espacio sólo estará en una dirección, lo cual corresponde a la dirección de flujo en la corriente. Si el contaminante estuviera en un lago profundo, entonces el espacio debería tener las tres direcciones.
Modelo. Discretizando tanto el espacio y el tiempo, e igualando la concentración a u(iΔx, kΔt) será aproximado por uik donde Δt = T/maxk, Δx=L/n y L es la longitud de la corriente. El modelo tendrá la forma general:
cambio en cantidad ≈ (cantidad entrando río arriba) – (cantidad saliendo rió abajo)
– (cantidad descomponiéndose en un intervalo de tiempo).
Esto es bosquejado en la figura debajo dónde el paso de tiempo no ha sido indicado
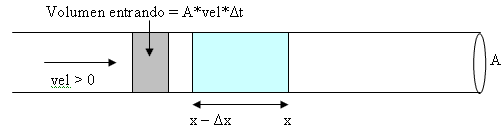
Figura. 4.29 Corriente contaminada
Asumiendo que la corriente está moviéndose de izquierda a derecha de tal manera que la velocidad es positiva, vel > 0. Haciendo A como el área de sección transversal de la corriente.
La cantidad entrando en el lado izquierdo del volumen A Δx (vel > 0) es
A Δt vel ui-1k
La cantidad saliendo en el lado derecho del volumen A Δx (vel > 0) es
-A Δt vel uik
Luego, el cambio en la cantidad a partir de la velocidad de la corriente es
A Δt vel ui-1k -A Δt vel uik
La cantidad de contaminante en el volumen A Δx en el tiempo kΔt es
A Δx uik
La cantidad de contaminante que se está descomponiendo, (dec es la velocidad de descomposición) es
A Δx Δt dec uik
El cambio durante el intervalo de tiempo en la cantidad de contaminante en el pequeño volumen A Δx:
A Δx uik+1 – A Δx uik = A Δt vel ui-1k – A Δt vel uik – A Δx Δt dec uik
Ahora, dividiendo por A Δx y resolviendo explícitamente para uik+1
Modelo Explicito de Diferencia Finita del flujo y descomposición de un contaminante
uik+1 = vel (Δt/Δx)ui-1k + (1- vel (Δt/Δx) – Δt dec) uik (4.55)
donde:
i = 1, …, n-1
k = 0, …, maxk-1
ui0 = dado para i = 1, …, n-1 (4.56)
uik = dado para i = 1, …, maxk (4.57)
La ecuación (4.56) es la concentración inicial, y (4.57) es la concentración lejos río arriba.
La ecuación (4.55) puede ser colocada en la versión matricial del método de diferencias finitas de primer orden. Por ejemplo, si la corriente es dividida en cuatro partes iguales, entonces n = 4 y la ecuación(4.55) puede ser escrita ya sea como tres ecuaciones escalares, o una ecuación vectorial de 3D:
Forma Escalar:
u1k+1 = vel (Δt/Δx)u0k + (1- vel (Δt/Δx) – Δt dec) u1k
u2k+1 = vel (Δt/Δx)u1k + (1- vel (Δt/Δx) – Δt dec) u2k
u3k+1 = vel (Δt/Δx)u2k + (1- vel (Δt/Δx) – Δt dec) u3k
Foma Vectorial
u1k+1 = A uk + b
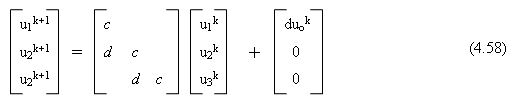
donde
d = vel (∆t/∆x) y c = 1 – d – dec ∆t
Una restricción sumamente importante en el paso de tiempo obliga a asegurar la estabilidad del algoritmo. Por ejemplo, considerar el caso n = 2 donde lo antedicho es una ecuación escalar, y tenemos el modelo de diferencia finita de primer orden más simple. Aquí a =1 – vel (∆t/∆x) – dec ∆t. Si a =1 – vel (∆t/∆x) – dec ∆t > 0 y vel, dec > 0, por lo que esta condición simple implicará que los productos de la matriz Ak convergen a la matriz cero. Esto asegura que no haya inestabilidad.
Condición de estabilidad para la ecuación (4.55)
a =1 – vel (∆t/∆x) – dec ∆t y vel, dec > 0
En el caso donde dec = 0, entonces a =1 – vel (∆t/∆x) > 0 de manera que el fluido que entra no debe viajar más que un paso en el espacio.
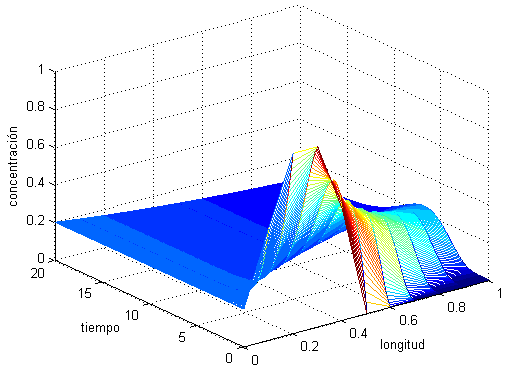
Figura: 4.30 Concentración como función de (t, x)
La segunda gráfica es una gráfica de contorno de la concentración en el tiempo versus el espacio. Aquí uno puede ver regiones del espacio que tienen concentración del contaminante entre ciertos niveles.
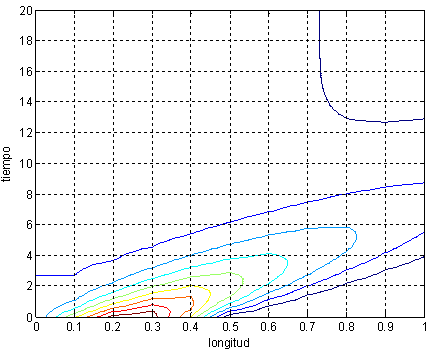
Figura 4.31 Contornos de concentración
La siguiente archivo.m Matlab produce un marco el cual no requiere un gran trato de memoria. Este código genera gráficas de la concentración versus espacio para una secuencia tiempos. En el modelo de contaminación del medio ambiente muestra el contaminante moviéndose a lo largo de corriente y descomponiéndose.
Otra forma para mirar la salida es coleccionando graficas de concentración versus el tiempo donde uno puede observar la concentración elevada moviéndose corriente abajo.
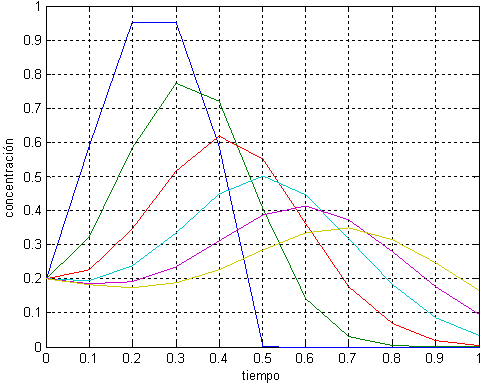
Figura 4.32 Concentraciones para incremento de tiempo
En el siguiente cálculo hacemos vel = 1.3, y esta, con las demas constantes iguales, viola la condición de estabilidad. Para el paso de tiempo 1/10 y una velocidad de flujo igual a 1., hace que el nivel de contaminante sea 1.3/10 unidades en el espacio lo cual es mayor a un paso de espacio.
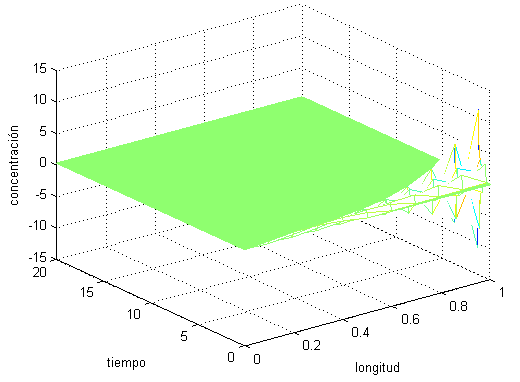
Figura 4.33 : Cálculo inestable con vel Δt > Δx
Discusión. El modelo discreto es preciso para adecuados tamaños de pasos pequeños.
A Δx uik+1 – A Δx uik = A Δt vel ui-1k – A Δt vel uik – A Δx Δt dec uik.
Dividiendo por AΔx Δt
(uik+1– uik)/Δt = vel (ui-1k – uik)/ Δx – dec uik
Aproximando a derivadas parciales de primer orden
ut(iΔx, kΔt + Δt/2) = -vel ux(iΔx – Δx/2, kΔt) – dec u(iΔx, kΔt).
La dispersión de contaminante es un proceso continuo, el cual podría ser modelado por una ecuación diferencial parcial y condiciones iniciales y de contorno:
ut = -vel ux – dec u,
u(x, 0) = dado
u(0, t) = dado
Este es análogo al modelo discreto por las ecuaciones (4.55), (4.56) y (4.57). En todos estos modelos, el tamaño de paso debe ser cuidadosamente seleccionado.
A menudo es dificultoso determinar el valor exacto de las constantes vel y dec. Exactamente cuál es el efecto que tiene los errores de medida, por decir de 10 %, sobre constante vel, dec o las condiciones inicial y límite? ¿Cual es la interacción es de los errores de medida con los errores numéricos? La tasa de flujo, vel, ciertamente no es siempre constante. Además, puede haber flujo de fluido en más de una dirección.
4.5.2 Contaminación de un lago
En el caso anterior un contaminante fue modelado como este fue dispersado bajo una corriente poco profunda. En este caso la concentración fue una función del tiempo y solo una variable de espacio, x. Si el contaminante fuese dispersado en un lago poco profundo, entonces la concentración sería una función de la posición en la superficie del lago, y así, la concentración sería una función de tiempo y dos variables de espacio, x e y.
Modelo. Fijando u(x,y,t) como la concentración de un contaminante. Suponer que este se está descomponiendo a una velocidad igual a dec unidades por tiempo, y está siendo dispersado a otra parte del lago por un viento conocido con vector de velocidad constante igual a (v1, v2).
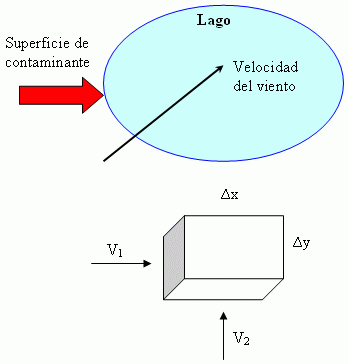
Figura 4.34 Esquema del lago
Siguiendo las derivaciones en el caso previo, pero ahora considerando ambas direcciones, obtenemos el modelo continuo y discreto. Hemos asumido que ambos componentes de la velocidad son no negativos a fin de que las concentraciones en los lados laterales contrarios al viento (el oeste y el sur) deben ser dadas. La cantidad entrando a la cara izquierda de la región rectangular es dada por
(T Δy) (v1 Δt) ui-1,jk
donde T es la profundidad, el volumen entrando es is (T Δy) (v1 Δt), y la concentración es ui-1,jk. El cambio total en la cantidad dentro de esta región rectangular sobre un intervalo de tiempo Δt es:
(T Δx Δy) (ui,jk+1 – ui,jk) = (T Δy) (v1 Δt) ui-1,jk – (T Δy) (v1 Δt) ui,jk
+ (T Δx) (v2 Δt) ui,j-1k – (T Δx) (v2 Δt) ui,jk
Δt dec (T Δx Δy) ui,jk (4.59)
En la ecuación diferencial parcial en el modelo continuo 2D los términos -v2 uy modelan la cantidad de contaminante entrando y saliendo por el tope y el fondo de la región rectangular
Modelo continuo 2Dpara el contaminante.
ut = – v1 ux – v2 uy – dec u, (1.1)
u(x,y,0) = dado (1.2)
u(x,y,t) = dado en el límite contrario al viento del lago. (1.3)
Modelo explicito en diferencia finita 2D para el contaminante
ui,jk+1 = v1 (Δt/Δx) ui-1,jk + v2 (Δt/Δy) ui,j-1k +
(1 – v1 (Δt/Δx) – v2 (Δt/Δy) – Δt dec)ui,jk (2.1)
ui,j0 = dado (2.2)
u0j y ui0 = dados (2.3)
Condición de Estabilidad.
1 – v1 (Δt/Δx) – v2 (Δt/Δy) – Δt dec > 0.
Metodo. Para ejecutar el modelo discreto, debe haber tres bucles anidados. El lazo exterior debe ser el lazo de tiempo (usar k), y los dos lazos interiores son para la cuadrícula del espacio (usando i y j). La orden i (la dirección x) y la j (la dirección y) no son importantes siempre que ambos esten dentro de la k (lazo de tiempo).
Implementación. El siguiente código Matlab simula un derramamiento grande de un contaminante a lo largo del límite sudoeste de un lago. La fuente del derramamiento se controla después de que 25 pasos de tiempo a fin de que la “nube” de contaminante que se mueve a través del lago sea bosquejado por la gráfica de contorno diferentes tiempos. El de código Matlab flujo2 genera el arreglo 3D de las concentraciones, y el código Matlab en mov2d.m genera una secuencia de gráficas de contorno.
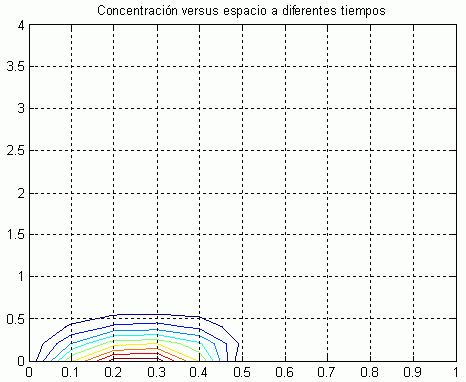
Figura 4.35 Simulación de la contaminación de un lago
Al hacer clic sobre la Figura 4.36, se desplaza la mancha de contaminante
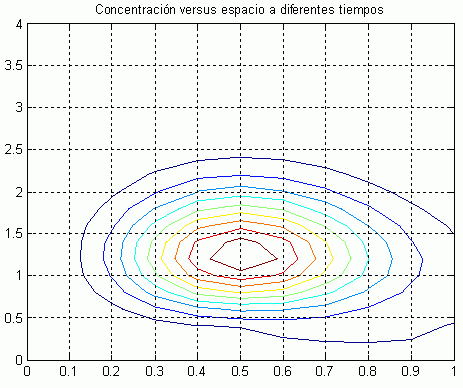
Figura 4.36 Concentración de contaminante versus tiempo
Comentario. Aquí hemos asumido que el único mecanismo para transferencia de contaminante es vía el movimiento del agua en el lago. Las partículas también pueden moverse en una manera similar como el flujo de calor moviéndose de regiones de concentraciones altas para las regiones de concentraciones inferiores. La contaminación del medio ambiente de agua subterránea es otro modelo relacionado. Aquí la velocidad del flujo será proporcional a la gradiente de la presión, así como la tasa de flujo de calor es proporcional a la gradiente de temperatura. Debido a que la constante de proporcionalidad depende del terreno subterráneo, esta no puede ser explícitamente conocida o considerarse constante!
