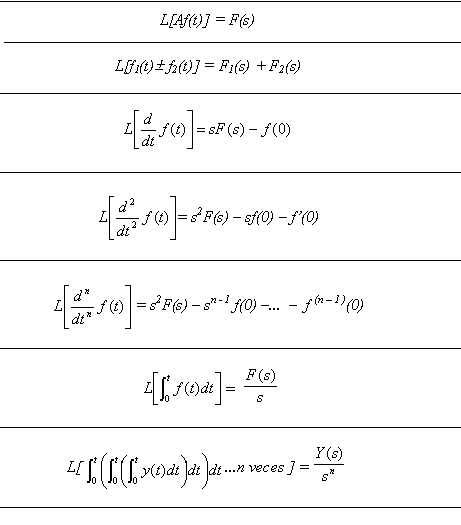Analizando el problema de control del tanque de calentamiento en el Cáp. 1, es evidente que la solución de las ecuaciones diferenciales será una de nuestras mayores tareas. El método de la transformada de Laplace proporciona una vía eficiente para solucionar ecuaciones diferenciales ordinarias, lineales con coeficientes constantes. Transformando una ecuación diferencial resulta una ecuación algebraica con la variable s reemplazando al tiempo como variable independiente. Resolviendo esta ecuación algebraica y haciendo la transformación inversa da la solución de la ecuación original.
4.1 EL CONCEPTO DE UNA TRANSFORMADA
Un ejemplo familiar de una transformada es un logaritmo. Por ejemplo, considerar la multiplicación de dos números tales como:
(643) (2,68) = …
Para resolverlo mediante logaritmos es necesario lo siguiente:
1. Tomar los logaritmos (hacer la transformación).
2. Sumar los logaritmos (solucionar el problema en un dominio matemático diferente). Notar que la complejidad del problema se ha reducido: Adición reemplaza a multiplicación.
3. Tomar el antilogaritmo (hacer la transformación inversa).
El problema transformado es resuelto en el paso 2, y luego en el paso 3 esta solución es convertida al dominio del problema original.
La transformada de Laplace tiene mucho en común con las transformadas logarítmicas. Las transformadas de Laplace son transformadas integrales y son transformadas para funciones en lugar de números.
Definimos:
f(t) = una función del tiempo t tal que f(t) = 0 para t < 0
![]()
L = un símbolo operacional que indica que la cantidad a la que procede debe
![]()
F(s) = transformada de Laplace de f(t)
Entonces la transformada de Laplace de f(t) está dada por
Donde L es el símbolo para “La transformada de Laplace de”.
Así pues, aplicar una transformada de Laplace a una ecuación diferencial equivale pasar del dominio del tiempo t a la variable compleja s + jw en el dominio de la s.
Para que al lector le sea más fácil comprenderlo, intente imaginarse que en lugar de vivir en nuestro mundo habitual en el que todos los fenómenos, tanto físicos como químicos, los referimos al tiempo utilizando como patrones los relojes, pasara a habitar otro mundo totalmente distinto en el que la referencia fuera una variable compleja s medida por patrones s en lugar de los relojes. Si consigue situarse en esta posición imaginaria, todos los razonamientos y conceptos que siguen y que están basados en la transformada de Laplace, le resultarán perfectamente comprensibles conceptualmente. (De hecho con una calculadora programada según la expresión básica de la transformada de Laplace o con el uso de un paquete de cálculo, es fácil pasar inmediatamente expresiones en el sistema t al sistema s).
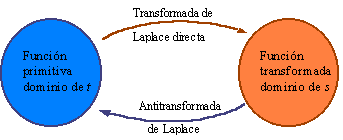
Fig. 4.1 Dominios t y s
Una vez que se ha obtenido la solución de la expresión algebraica en función de la variable s, bastará buscar la transformada inversa de Laplace (antitransformada) con el fin de obtener la solución de la ecuación diferencial en el dominio del tiempo. Se expresa del modo siguiente:
L-1 [F(s)] = f(t) (4.2)
Ejemplo 4.1
Encontrar la transformada de Laplace de la función: f(t) = 1
De acuerdo a la Ec. 4.1
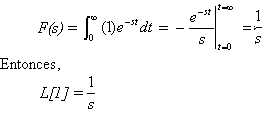
Análogamente, la transformada de una constante sería
![]()
En la Tabla 4.1 se encuentran resueltas las transformadas de las funciones más comunes.
TABLA 4.1 Tabla de transformadas de Laplace
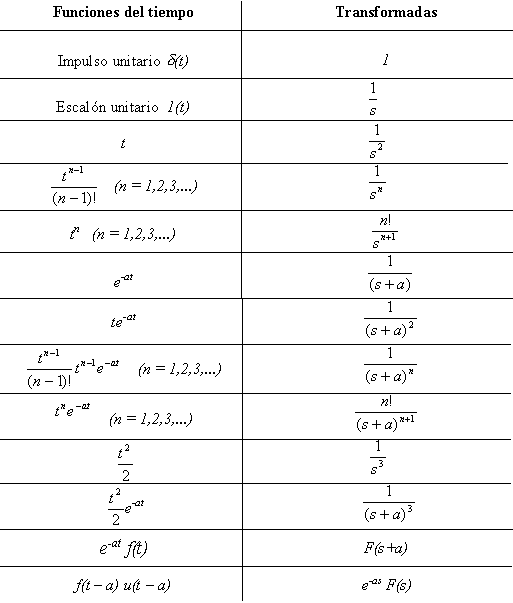
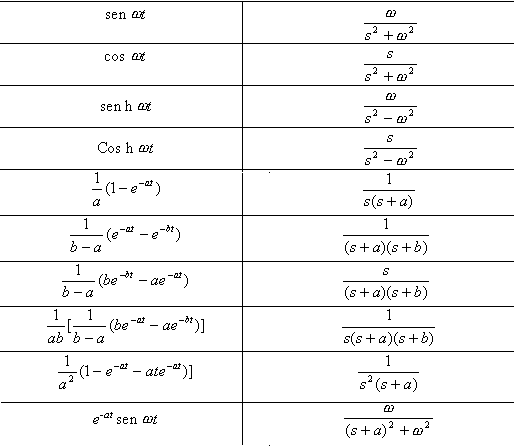
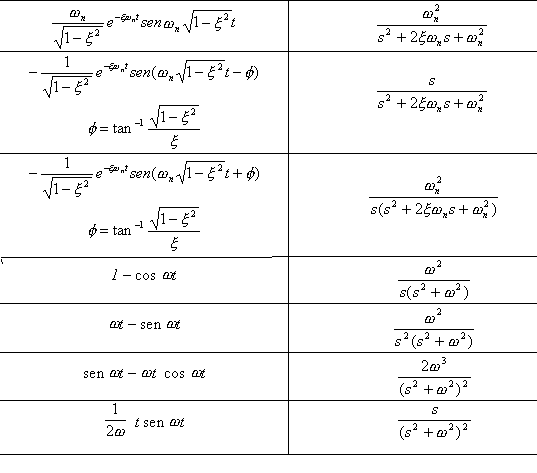
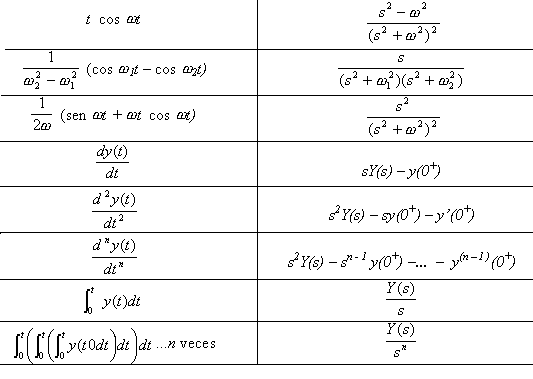
4.1.1 Consideraciones importantes de la Transformada de Laplace
Hay varios factores importantes que se deben considerar:
1. La transformada de Laplace F(s) no contiene información acerca del comportamiento de f(t) para t < 0. esto no es una limitación para el estudio de sistemas de control ya que t representa la variable tiempo y el estudio del comportamiento de sistemas se hace solamente para t > 0. en realidad, las variables y sistemas son definidos usualmente tal que f(t) º 0 para t < 0. esto quedará claro con el estudio de los ejemplos específicos.
2. Puesto que la transformada de Laplace es definida en la Ec. (4.1) por una integral impropia, esta no existirá para todas las funciones f(t).
3. la transformada de Laplace es lineal. En notación matemática será:
L[Af1(t) + Bf2(t)] = A L[f1(t)] + B L[f2(t)] (4.4)
Donde A y B son constantes, y f1, f2 son dos funciones de t
4. El operador de Laplace transforma una función de la variable t a una función de la variable s. La variable t es eliminada mediante la integración.
4.2 TRANSFORMADA DE UNA DERIVADA
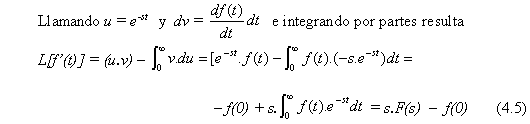
esta última, aplicada reiteradamente a una derivada enésima, daría
L[fn(t)] = snF(s) – sn – 1 f(0) – sn – 2 f’(0) – . . . – fn-1(0) (4.6)
y con las condiciones iniciales supuestas nulas resulta:
L[f n(t)] = sn F(s) (4.7)
Encontrar la transformada de Laplace de la función x(t) la cual satisface la ecuación diferencial y las condiciones iniciales
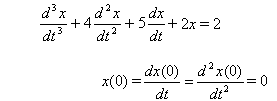
Es permisible matemáticamente tomar la transformada de Laplace de una ecuación diferencial e igualarlos, ya que igualdad de funciones implica igualdad de sus transformadas. Haciendo esto, se obtiene
s3X(s) – s2x(0) – sx¢(0) – x¢¢(0) + 4[s2X(s) – sx(0) – x¢(0)]
![]()
donde X(s) = L[x(t)]. Se ha hecho uso de la propiedad de linealidad y del hecho de que solamente son de interés valores positivos de t. Insertando las condiciones iniciales y resolviendo para X(s)
![]()
4.3 TRANSFORMADA DE UNA INTEGRAL
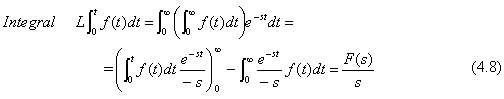
Es decir, la transformada de Laplace convierte la operación de derivar en una multiplicación por la variable s y la operación de integrar en una división por la misma variable s, siempre que naturalmente las condiciones iniciales sean nulas.
4.4 TRANSFORMADA INVERSA
En las secciones previas se ha dado f(t) y el problema ha sido determinar su transformada de Laplace F(s). En esta sección se considera el problema de hallar f(t) cuando se conoce F(s); el proceso es conocido como inversión. Esta operación es comúnmente denotada por:
f(t) = L-1[F(s)] (4.9)
En la mayoría de los casos, la transformación inversa se puede obtener de la tabla de transformadas tales como las mostradas en la Tabla (4.1). en esta tabla, dos funciones de t no tienen la misma transformada de Laplace o dos funciones de s no tienen la misma transformada inversa. En general, la transformada inversa es única si no son tomadas en cuenta las funciones nulas, tales como las funciones cuya integral con respecto al tiempo es cero.
4.5 PROPIEDADES DE LAS TRANSFORMADAS
Las propiedades de la transformada de Laplace son las siguientes:
– Linealidad L[f1 (t) ± f2 (t)] = F1(s) ± F2(s) (4.10)
– Permutabilidad L[k.f(t)] = k.L[f(t)] (4.11)
![]()
4.5.1 Teorema del valor inicial
Permite conocer el valor de una función en el origen sin necesidad de calcular su antitransformada y sustituir en ella la variable independiente por 0.
Se sabe que, conocida la función y(t), la transformada de Laplace de su derivada es:
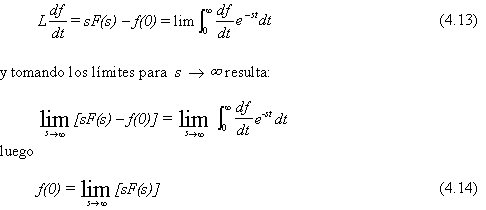
4.5.2 Teorema del valor final
De una forma análoga a la anterior se desea saber el valor de una función en el infinito, y no es posible o bien no se desea calcular su transformada inversa.
Procediendo como antes se busca la transformada de Laplace de su derivada y se toman límites para s ![]() 0, con lo cual resulta:
0, con lo cual resulta:
![]()
luego
![]()
4.5.3 Teorema del retardo puro
Cumple la igualdad: L[f(t – T)] = e-sT F(s) siendo el retardo puro la función
f = e-sT y T una constante

Si se impone que las condiciones iniciales son nulas en la función primitiva y en sus derivadas, resulta:
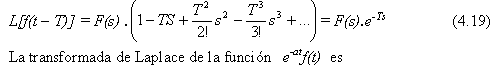
L[e-atf(t)] = F(s + a) (4.20)
o bien deshaciendo la transformación
L-1 [F(s + a)] = e-at f(t) = e-at L-1 [F(s)] (4.21)
que puede considerarse homónima del teorema del retardo puro, cambiando los dominios t y s.
Ejemplo 4.4
Valores inicial y final de una función f(t) cuya transformada de Laplace es:

Si se deseara conocer la forma de arranque de la curva en el origen, se procedería del modo siguiente
En el dominio del tiempo
![]()
En el instante inicial t ![]() 0, se producen variaciones rápidas de la derivada y puede suponerse que ésta tiende a infinito p
0, se producen variaciones rápidas de la derivada y puede suponerse que ésta tiende a infinito p ![]() ¥. Luego
¥. Luego
![]()
Lo que indica que el origen la curva se comporta como si fuera equivalente a la función.
TABLA 4.2 Propiedades de las transformadas de Laplace