Si analizamos el Ejemplo 4.2, hay dos puntos importantes con respecto a este ejemplo. En primer lugar, la aplicación de la transformación trae como resultado una ecuación la cual es resuelta para la función desconocida por medios puramente algebraicos. Segundo, y más importante, si la función x(t) la cual tiene la transformada de Laplace 2/s(s3 + 4s2 + 5s + 2) fuese conocida, podríamos tener la solución a la ecuación diferencial y las condiciones de frontera. Esto sugiere un procedimiento para resolver ecuaciones diferenciales.
En el método de la transformada de Laplace para la solución de ecuaciones diferenciales, la función es convertida a sus transformadas y las ecuaciones resultantes son resueltas algebraicamente para la función desconocida. Esto es mucho más fácil que resolver una ecuación diferencial. Nosotros obviamente no podemos esperar construir una tabla conteniendo las transformadas de Laplace de cada función f(t) la cual posee una transformada. En cambio podríamos desarrollar métodos para expresar transformadas complicadas, tal como X(s) del Ejemplo 4.2, en términos de transformadas simples las cuales pueden encontrarse en la Tabla 4.1. Por ejemplo, se puede verificar fácilmente que la solución a la ecuación diferencial y condiciones de frontera del Ejemplo 4.2 es
x(t) = 1 – 2te-1 – e-2t (5.1)
La transformada de Laplace de x, usando la Ec. (5.1) y la Tabla (4.1), es
![]()
La ecuación X(s) = 2/s(s3 + 4s2 + 5s + 2) es el resultado de poner la Ec. (5.2) sobre un denominador común y muchas veces es difultuoso encontrar x(t) a partir de esta ecuación, requiriéndose un método para expandir la forma de denominador común a la forma separada dada en la Ec. (5.2). Este método es dado por la técnica de fracciones parciales que se verá más adelante.
5.1 Inversión por fracciones parciales
En problemas de análisis de teoría de control, F(s), la transformada de Laplace de f(t), frecuentemente es de la forma
![]()
donde las A(s) y B(s) son polinomios en s, y el grado de B(s) es menor de A(s). Si F(s) se descompone en sus componentes,
F(s) = F1(s) + F2(s) + . . . + Fn(s) (5.4)
y si las transformadas inversas de Laplace de F1(s), F2(s) , . . . , Fn(s) son obtenidas fácilmente, entonces
L-1[F(s)] = L-1[F1(s)] + L-1[F2(s)] +. . . + L-1[Fn(s)] (5.5)
= f1(t) + f2(t) + . . . + fn(t) (5.6)
donde f1(t), f2(t), . . ., fn(t) son las transformadas inversas de Laplace de F1(s), F2(s) , . . . , Fn(s), respectivamente. La transformada inversa de Laplace así obtenida F(s) es única, excepto posiblemente en puntos donde la función de tiempo es discontinua. Toda vez que la función de tiempo sea continua, las funciones del tiempo f(t) y sus transformadas de Laplace F(s) tienen una correspondencia univoca.
La ventaja del procedimiento de expansión en fracciones parcialices es que los términos individuales de F(s), resultantes de la expansión en forma de fracciones parciales, son funciones muy simples de s. En consecuencia no es necesario recurrir a una tabla de transformadas de Laplace, si se memorizan algunos pares de transformadas de Laplace simples. Conviene señalar, sin embargo, que al aplicar la técnica de expansión en fracciones parciales en búsqueda de la transformada inversa de Laplace de F(s) = B(s)/A(s) deben conocerse previamente las raíces del polinomio denominador A(s). Es decir, este método no se aplica hasta que se ha factorizado el polinomio denominador.
En la expansión de F(s) = B(s)/A(s) en forma de fracciones parciales, es importante que la potencia más elevada de s en A(s) sea mayor que la potencia de s en B(s). Si ese no es el caso, el numerador B(s) debe dividirse entre el denominador A(s) para producir un polinomio en s más un resto (una relación de polinomios en s cuyo numerador sea de grado menor que el denominador). (Para detalles ver el Ejemplo 5.2)
5.1.1 Expansión en fracciones parciales cuando F(s) contiene únicamente polos distintos
Sea F(s) escrita en su forma factorizada
![]()
donde p1, p2, . . ., pn y z1, z2, . . ., zm son cantidades reales o complejas, para cada complejo p o z, debe aparecer el respectivo conjugado de pi o zi. Si F(s) contiene solamente polos distintos, puede expandirse en una suma de fracciones parciales simples, es decir:
![]()
donde ak (k = 1, 2, . . ., n) son constantes. El coeficiente ak se denomina residuo en el polo de s = – pk. El valor de ak puede hallarse multiplicando ambos miembros de la Ec. (5.8) por (s + pk) y haciendo s = – pk, lo que da
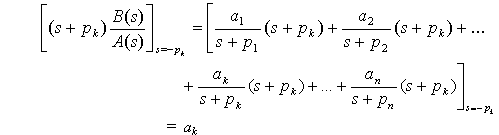
Como puede verse, todos los términos expandidos desaparecen, excepto ak. Entonces se halla que el residuo es

Nótese que, como f(t) es una función real del tiempo, si p1 y p2 son complejos conjugados, los residuos de a1 o a2 también son complejos conjugados. Sólo uno de los conjugados, a1 o a2 debe evaluarse, ya que el otro se conoce automáticamente.
Como
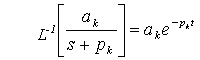
Se obtiene f(t) como
![]()
Hallar la transformada inversa de Laplace de
![]()
La expansión de F(s) en fracciones parciales es
![]()
donde a1 y a2 se determinan utilizando la Ec. (5.9).
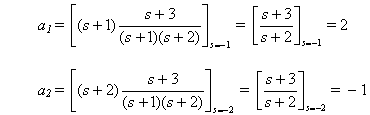
Entonces
f(t) = L-1[F(s)]
![]()
= 2e – t – e – 2 t (t ³ 0)
Obtener la transformada inversa de Laplace de
![]()
Nótese que el polinomio denominador puede factorizarse como
s2 + 2s + 5 = (s + 1 + j2)(s + 1 – j2)
Si la función F(s) incluye un par de polos complejos conjugados, es conveniente no expandir en las fracciones parciales habituales, sino en una suma de una función seno y una función coseno amortiguadas.
Considerando que s2 + 2s + 5 = (s + 1)2 + 22 y colocando las transformadas de Laplace de e – µ t sen w t y e – µ t cos w t, se escribe
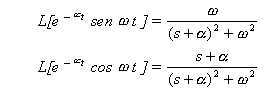
De aquí que:
f(t) = L-1[F(s)]
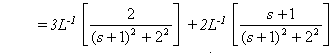
= 5e – t sen 2t + 2e – t cos 2t (t ³ 0)
5.1.2 Expansión en fracciones parciales cuando F(s) tiene polos múltiples
En lugar de tratar el caso general, se utiliza un ejemplo para mostrar cómo obtener la expansión de F(s) en fracciones parciales.
Sea la siguiente F(s):
![]()
La expansión en fracciones parciales de esta F(s) cubre tres términos
![]()
donde b1, b2 y b3 se determinan como sigue. Multiplicando ambos miembros de esta última ecuación por (s + 1)3, se tiene
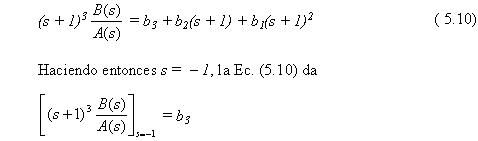
También diferenciando ambos miembros de la Ec. (5.10) con respecto a s se obtiene
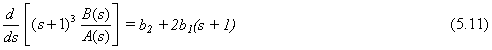
Si se hace s = – 1 en la Ec. (5.11), entonces
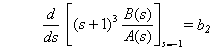
Diferenciando ambos miembros de la Ec. (5.11) respecto a s, el resultado es
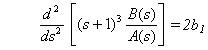
Del análisis precedente se puede ver que los valores b1, b2 y b3 pueden determinarse sistemáticamente del siguiente modo:
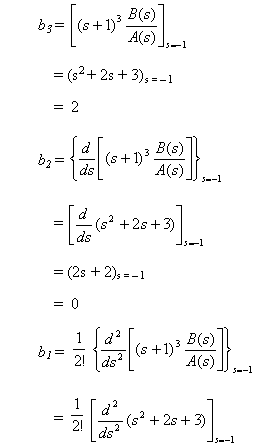
= ½ (2) = 1
Así, se tiene
f(t) = L-1[F(s)]
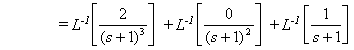
= t2 e – t + 0 + e – t
= (t2 +1) e – t (t ³ 0)
5.1.3 Descomposición en fracciones parciales usando MATLAB
Una herramienta importante en el diseño y análisis de sistemas de control es MATLAB. Comenzaremos viendo su aplicación en la descomposición de expresiones en fracciones parciales, para lo cual consideraremos la razón de dos polinomios b(s) y a(s) de la forma
![]()
donde a(1) ¹ 0, pero algún a(i) y b(j) pueden ser ceros.
Los vectores fila num y den especifican los coeficientes del numerador y del denominador de la función de transferencia. Es decir,
num = [b(1) b(2) … b(n)]
den = [a(1) a(2) … a(n)]
La orden
[r,p,k] = residue(num,den)encuentra los residuos, los polos y los términos directos de una descomposición en fracciones parciales del cociente de dos polinomios B(s) y A(s). La descomposición en fracciones parciales de B(s)/A(s) viene dada por
![]()
Descomponer en fracciones parciales la siguiente expresión
![]()
Solución
Para esta función,
num = [2 5 3 6]
den = [1 6 11 6]
La orden
[r,p,k] = residue(num,den)da el siguiente resultado
>> num = [2 5 3 6] >> den = [1 6 11 6] >> [r,p,k] = residue(num,den)
r =
-6.0000
-4.0000
3.0000
p =
-3.0000
-2.0000
-1.0000
k =
2
>>
(Observe que los residuos se devuelven en un vector columna r, la localización de los polos en un vector columna p y los términos directos en un vector fila k). Esta es la respuesta en MATLAB de la siguiente descomposición en fracciones parciales de B(s)/A(s):
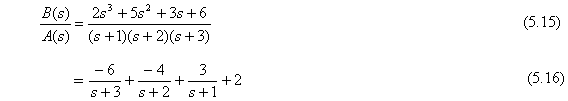
La orden
[num,den]=residue (r,p,k)donde r, p, k son dadas en la anterior salida de MATLAB, convierte la descomposición en fracciones parciales al polinomio cociente B(s)/A(s) como sigue:
>> [num,den]=residue (r,p,k)
num =
2.0000 5.0000 3.0000 6.0000
den =
1.0000 6.0000 11.0000 6.0000
>>
Lo cual equivale a la Ec. (5.14)
![]()
5.3 RESOLUCIÓN DE ECUACIONES DIFERENCIALES LINEALES INVARIANTES EN EL TIEMPO
El método de la transformada de Laplace brinda la solución completa (la solución particular más la complementaria) de ecuaciones diferenciales ordinarias invariantes en el tiempo. Los métodos clásicos para hallar la solución completa de una ecuación diferencial, requieren evaluar las constantes de integración a partir de las condiciones iniciales. En el caso de la transformada de Laplace, empero, no es necesario calcular las constantes de integración a partir de las condiciones iniciales, ya que estas quedan incluidas automáticamente en la transformada de Laplace de la ecuación diferencial.
Si todas las condiciones iniciales son cero, la transformada de Laplace de la ecuación diferencial, se obtiene substituyendo simplemente d/dt por s, d2/dt2 por s2, etc.
El método para la solución de ecuaciones diferenciales ordinarias con coeficientes constantes con la transformada de Laplace comprende:
- Tomar la transformada de ambos lados de la ecuación, en este punto se incorporan las condiciones iniciales en las transformadas de las derivadas.
- Resolver algebraicamente la ecuación resultante para la transformada de Laplace de la función desconocida.
- Encontrar la función de t la cual tiene la transformada de Laplace obtenida en el paso 2. esta función satisface la ecuación diferencial y las condiciones iniciales y es la solución deseada.
Resolver
x’ + 3x = 0
x(0) = 2
Enumerando las etapas de acuerdo a la discusión anterior:
1. sX(s) – 2 + 3X(s) = 0
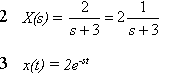
Hallar x(t) de la ecuación diferencial
x” + 3x¢ + 2x = 0 x(0) = a x¢ (0) = b
donde a y b son constantes.
Denotando la transformada de Laplace de x(t) por X(s), o sea
L[x(t)] = X(s)
se obtiene
L[x¢ ] = sX(s) – x (0)
L[x¢¢ ] = s2X(s) – sx(0) – x¢(0)
Y entonces la ecuación diferencial dada se convierte en
[s2X(s) – sx(0) – x¢(0)] +3[sX(s) – x(0)] + 2X(s) = 0
Substituyendo las condiciones iniciales en esta última ecuación,
[s2X(s) – as – b] + 3[sX(s) – a] + 2X(s) = 0
o
(s2 + 3s + 2)X(s) = as + b + 3a
Despejando el valor de X(s), se tiene
![]()
La transformad inversa de Laplace de X(s) da
![]()
= (2a + b)e – t – ( a + b) e – 2 t (t ³ 0)
Que es la solución de la ecuación diferencial propuesta. Nótese que en la solución aparecen las condiciones iniciales a y b. Así, x(t) no tiene constantes indeterminadas.
Encontrar la solución x(t) de la ecuación diferencial
x” + 2x’ + 5x = 3 x(0) = 0 x’ (0) = 0
Considerando que L[3] = 3/s, x(0) = 0, x’ (0) = 0, la transformada de Laplace de la ecuación diferencial es
s2X(s) + 2sX(s) + 5X(s) = 3/s
Al resolver para despejar X(s), se halla
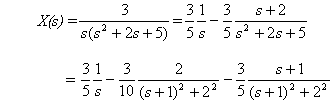
Por lo tanto, la transformada inversa de Laplace es
x(t) = L– 1[X(s)]
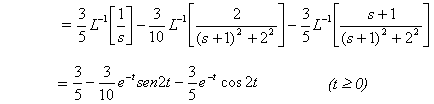
Resolver la ecuación diferencial siguiente para las condiciones iniciales
y(0) = – 1, y’ (0) = 2
y ” + 3y’ + 2y – 5 = 0
La transformada de Laplace es:
y” = s2Y(s) – sy(0) – y¢(0) = s2Y(s) + s – 2
y’ =sY(s) – y(0)
luego:
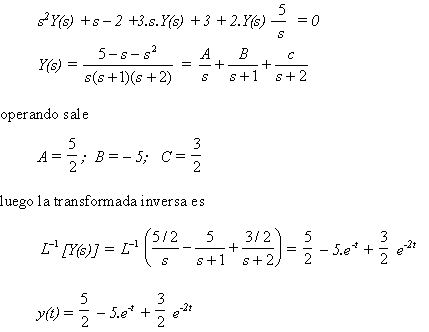
5.5 DESCOMPOSICIÓN EN FRACCIONES PARCIALES USANDO MATLAB
Una herramienta importante en el diseño y análisis de sistemas de control es MATLAB. Comenzaremos viendo su aplicación en la descomposición de expresiones en fracciones parciales, para lo cual consideraremos la razón de dos polinomios b(s) y a(s) de la forma
![]()
donde a(1) ¹ 0, pero algún a(i) y b(j) pueden ser ceros.
Los vectores fila num y den especifican los coeficientes del numerador y del denominador de la función de transferencia. Es decir,
num = [b(1) b(2) … b(n)]
den = [a(1) a(2) … a(n)]
La orden
[r,p,k] = residue(num,den)encuentra los residuos, los polos y los términos directos de una descomposición en fracciones parciales del cociente de dos polinomios B(s) y A(s). La descomposición en fracciones parciales de B(s)/A(s) viene dada por
![]()
Descomponer en fracciones parciales la siguiente expresión
![]()
Solución
Para esta función,
num = [2 5 3 6]
den = [1 6 11 6]
La orden
[r,p,k] = residue(num,den)da el siguiente resultado
>> num = [2 5 3 6] >> den = [1 6 11 6] >> [r,p,k] = residue(num,den)
r =
-6.0000
-4.0000
3.0000
p =
-3.0000
-2.0000
-1.0000
k =
2
>>
(Observe que los residuos se devuelven en un vector columna r, la localización de los polos en un vector columna p y los términos directos en un vector fila k). Esta es la respuesta en MATLAB de la siguiente descomposición en fracciones parciales de B(s)/A(s):
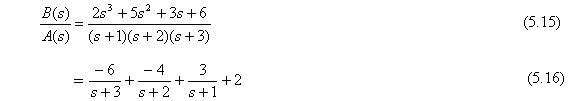
La orden
[num,den]=residue (r,p,k)donde r, p, k son dadas en la anterior salida de MATLAB, convierte la descomposición en fracciones parciales al polinomio cociente B(s)/A(s) como sigue:
>> [num,den]=residue (r,p,k)
num =
2.0000 5.0000 3.0000 6.0000
den =
1.0000 6.0000 11.0000 6.0000
>>
![]()
